Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Параллелограмм. Свойства параллелограмма». Материал предназначен для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Параллелограмм. Свойства параллелограмма
Вариант 1
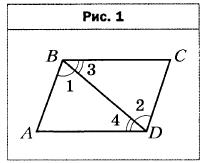
- В четырёхугольнике ABCD (рис. 1) ∠1 = ∠2, ∠3 = ∠4. Докажите, что четырёхугольник ABCD — параллелограмм.
- Периметр параллелограмма равен 56 см. Найдите его стороны, если одна из них на 6 см больше другой.
- Периметр параллелограмма равен 126 см. Найдите его стороны, если две из них относятся как 4 : 5.
- Найдите углы параллелограмма, если:
1) один из его углов равен 46°; 2) сумма двух его углов равна 186°; 3) один из его углов на 56° больше другого; 4) один из его углов в 3 раза меньше другого; 5) два его угла относятся как 5 : 7. - Даны два параллелограмма ABCD и KMNP. Могут ли одновременно выполняться неравенства: ∠А > ∠К и ∠B > ∠M?
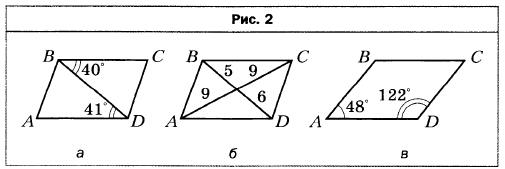
- На рисунке 2 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Диагонали параллелограмма ABCD пересекаются в точке О. Найдите разность периметров треугольников COD и AOD, если АВ = 7 см, ВС = 4 см.
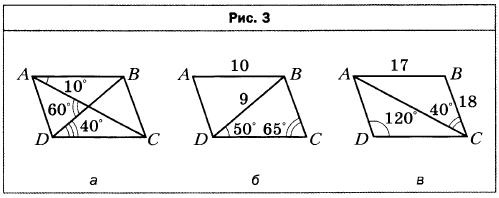
- На рисунке 3 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неправильно (длины отрезков даны в сантиметрах).
- Биссектрисы углов А к В параллелограмма ABCD пересекаются в точке О. Найдите сторону АВ параллелограмма, если ОА = 8 см и ∠ABO = 30°.
- В параллелограмме ABCD известно, что АВ = 7 см, AD = 12 см. Биссектриса угла А пересекает сторону ВС в точке Е. Найдите отрезки BE и ЕС.
- Биссектриса угла А параллелограмма ABCD делит сторону CD в отношении 1:3, считая от вершины угла С. Найдите стороны параллелограмма, если его периметр равен 84 см.
- В параллелограмме ABCD угол А равен 60°. Высота BE делит сторону AD в отношении 3 : 8, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 68 см.
- Два угла параллелограмма относятся как 1:5. Найдите угол между высотами параллелограмма, проведёнными из вершины острого угла.
- В параллелограмме ABCD проведены высоты ВМ и ВК. Найдите периметр параллелограмма, если ВМ = 6 см, ВК = 9 см, ∠ADC = 150°.
- На основании равнобедренного треугольника отмечена произвольная точка и через неё проведены прямые, параллельные его боковым сторонам. Найдите периметр полученного параллелограмма, если боковая сторона равнобедренного треугольника равна 6 см.
- Постройте параллелограмм ABCD, если заданы точки М, N и К — середины сторон АВ, ВС и CD соответственно.
- Постройте параллелограмм ABCD, если заданы его вершины А и В и точка О — точка пересечения диагоналей параллелограмма.
Вариант 2
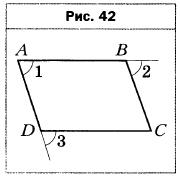
- В четырёхугольнике ABCD (рис. 42) ∠1 = ∠2 = ∠3. Докажите, что четырёхугольник ABCD — параллелограмм.
- Периметр параллелограмма равен 84 см. Найдите стороны параллелограмма, если одна из них на 12 см меньше другой.
- Периметр параллелограмма равен 90 см. Найдите его стороны, если две из них относятся как 2:3.
- Найдите углы параллелограмма, если:
1) один из его углов равен 52°; 2) сумма двух его углов равна 174°; 3) один из его углов на 28° больше другого; 4) один из его углов в 4 раза меньше другого; 5) два его угла относятся как 4:5. - Даны два параллелограмма ABCD и EFGH. Могут ли одновременно выполняться неравенства: ∠B < ∠F и ∠C < ∠G?
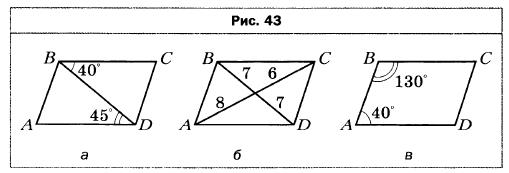
- На рисунке 43 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Диагонали параллелограмма ABCD пересекаются в точке О. Найдите разность периметров треугольников ВОС и COD, если АВ = 9 см, AD = 14 см.
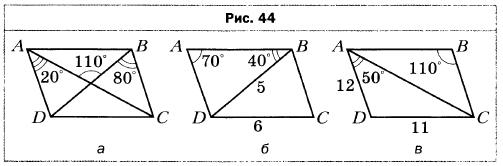
- На рисунке 44 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Биссектрисы углов С и D параллелограмма ABCD пересекаются в точке О. Найдите отрезок СО, если CD = 10 см и ∠DCO = 60°.
- Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К, ВК = 4 см и КС = 3 см. Найдите стороны параллелограмма.
- Биссектриса угла В параллелограмма ABCD делит сторону AD в отношении 2:3, считая от вершины угла А. Найдите стороны параллелограмма, если его периметр равен 42 см.
- В параллелограмме ABCD угол А равен 120°. Высота АК делит сторону CD в отношении 3 : 5, считая от вершины тупого угла. Найдите стороны параллелограмма, если его периметр равен 108 см.
- Два угла параллелограмма относятся как 3 : 7. Найдите угол между высотами параллелограмма, проведёнными из вершины тупого угла.
- В параллелограмме ABCD проведены высоты AM и AN. Найдите периметр параллелограмма, если AM -= 8 см, AN = 11 см, ∠BCD = 30°.
- На основании равнобедренного треугольника отмечена произвольная точка и через неё проведены прямые, параллельные его боковым сторонам. Периметр полученного параллелограмма равен 24 см. Найдите боковую сторону треугольника.
- Постройте параллелограмм ABCD, если заданы его вершина А и точки Ми N — середины сторон АВ и CD соответственно.
- Постройте параллелограмм ABCD, если заданы его вершина А, точка М — середина стороны АВ, точка О — точка пересечения диагоналей параллелограмма.
Вариант 3
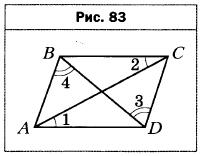
- В четырёхугольнике ABCD (рис. 83) ∠1 = ∠2, ∠3 = ∠4. Докажите, что четырёхугольник ABCD — параллелограмм.
- Периметр параллелограмма равен 80 см. Найдите стороны параллелограмма, если одна из них на 14 см меньше другой.
- Периметр параллелограмма равен 98 см. Найдите его стороны, если две из них относятся как 4:3.
- Найдите углы параллелограмма, если:
1) один из его углов равен 63°; 2) сумма двух его углов равна 134°; 3) один из его углов на 44° меньше другого; 4) один из его углов в 11 раз меньше другого; 5) два его угла относятся как 5:13. - Даны два параллелограмма ABCD и PKTF. Могут ли одновременно выполняться неравенства: ∠C > ∠T и ∠D > ∠F4
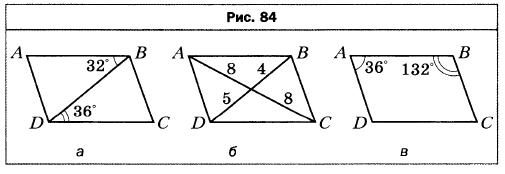
- На рисунке 84 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Диагонали параллелограмма ABCD пересекаются в точке О. Найдите разность периметров треугольников АОВ и ВОС, если CD =11 см, AD = 6 см.
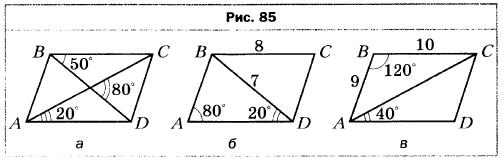
- На рисунке 85 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке О. Найдите сторону ВС параллелограмма, если ОС = 6 см и ∠BCO = 60°.
- В параллелограмме ABCD известно, что AD = 8 см, CD = 11 см. Биссектриса угла D пересекает сторону АВ в точке К. Найдите отрезки АК и КВ.
- Биссектриса угла С параллелограмма ABCD делит сторону АВ в отношении 1 : 4, считая от вершины угла А. Найдите стороны параллелограмма, если его периметр равен 72 см.
- В параллелограмме ABCD угол В равен 60°. Высота АН делит сторону ВС в отношении 4 : 7, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 76 см.
- Два угла параллелограмма относятся как 5 : 7. Найдите угол между высотами параллелограмма, проведёнными из вершины острого угла.
- В параллелограмме ABCD проведены высоты ВН и DE. Найдите периметр параллелограмма, если ВН = 10 см, DE = 7 см, ∠ABC = 150°.
- На основании равнобедренного треугольника отмечена произвольная точка и через неё проведены прямые, параллельные его боковым сторонам. Найдите периметр полученного параллелограмма, если боковая сторона равнобедренного треугольника равна 10 см.
- Постройте параллелограмм ABCD, если заданы точки М и N — середины сторон АВ и ВС соответственно и точка О — точка пересечения диагоналей параллелограмма.
- Постройте параллелограмм ABCD, если заданы его вершина А, точка М — середина стороны ВС, точка О — точка пересечения диагоналей параллелограмма.
Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Параллелограмм. Свойства параллелограмма». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!