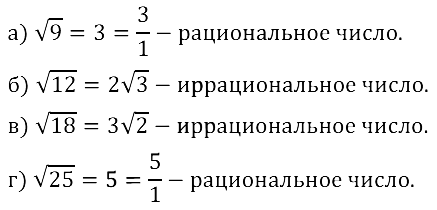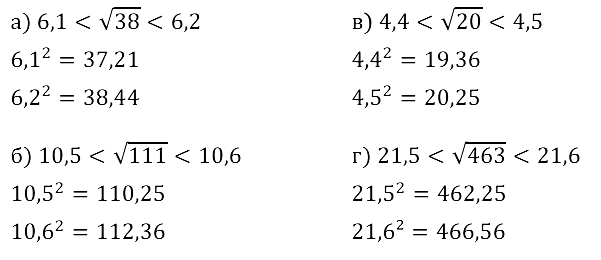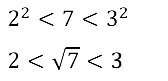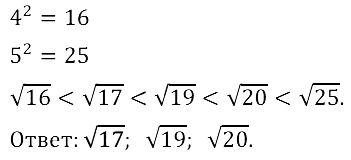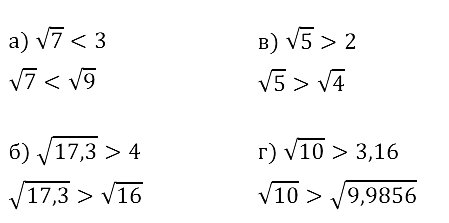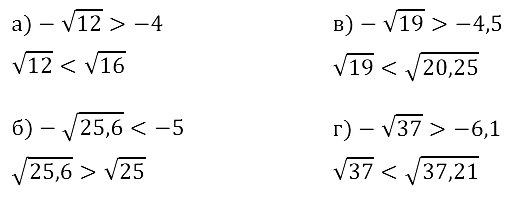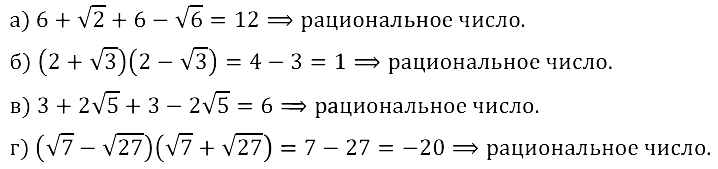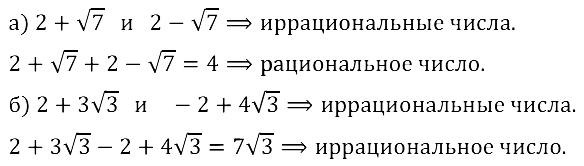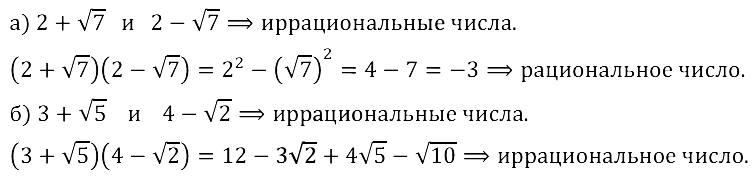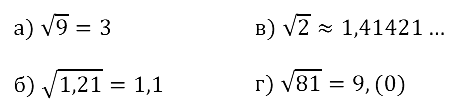Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 2. ФУНКЦИЯ у = √x. СВОЙСТВА КВАДРАТНОГО КОРНЯ. § 12. Иррациональные числа. ОТВЕТЫ на упражнения 12.1 — 12.17. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 12.1 — 12.17)
§ 12. Иррациональные числа
Задание № 12.1. Является ли данное число иррациональным: a) √9; б) √12; в) √18; г) √25 ?
Задание № 12.2. Проверьте справедливость соотношения:
а) 6,1 < √38 < 6,2; б) 10,5 < √111 < 10,6; в) 4,4 < √20 < 4,5; г) 21,5 < √463 < 21,6.
Задание № 12.3. Между какими целыми числами находится число √7 ?
Задание № 12.4. Найдите три иррациональных числа, которые находятся между числами 4 и 5.
Задание № 12.5. Сравните числа: а) √7 и 3; б) √17,3 и 4; в) √5 и 2; г) √10 и 3,16.
Задание № 12.6. а) –√12 и –4; б) –√25,6 и –5; в) –√l9 и –4,5; г) –√37 и –6,1.
Задание № 12.7. Докажите, что:
а) сумма иррациональных чисел 6 + √2 и 6 – √2 является рациональным числом;
б) произведение иррациональных чисел 2 + √3 и 2 – √3 является рациональным числом;
в) сумма иррациональных чисел 3 + 2√5 и 3 – 2√5 является рациональным числом;
г) произведение иррациональных чисел √7 – √27 и √7 + √27 является рациональным числом.
Задание № 12.8. а) Приведите пример двух иррациональных чисел, сумма которых — рациональное число.
б) Приведите пример двух иррациональных чисел, сумма которых — иррациональное число.
Задание № 12.9. а) Приведите пример двух иррациональных чисел, произведение которых — рациональное число.
б) Приведите пример двух иррациональных чисел, произведение которых — иррациональное число.
Задание № 12.10.
Задание № 12.11.
Задание № 12.12.
Задание № 12.13.
Задание № 12.14.
Задание № 12.15.
Задание № 12.16.
Задание № 12.17.
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 2. ФУНКЦИЯ у = √x. СВОЙСТВА КВАДРАТНОГО КОРНЯ. § 12. Иррациональные числа. ОТВЕТЫ на упражнения 12.1 — 12.17. Вернуться в ОГЛАВЛЕНИЕ.