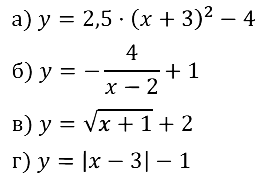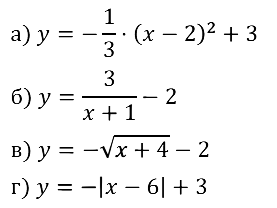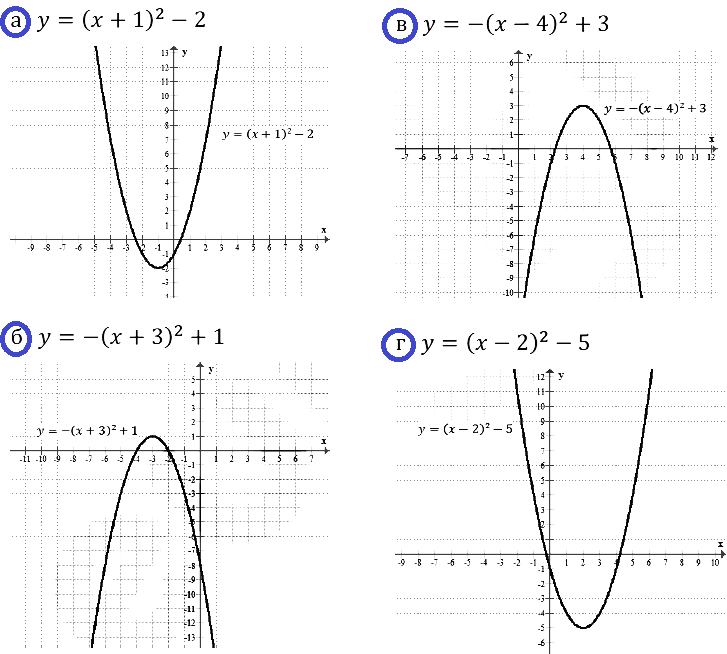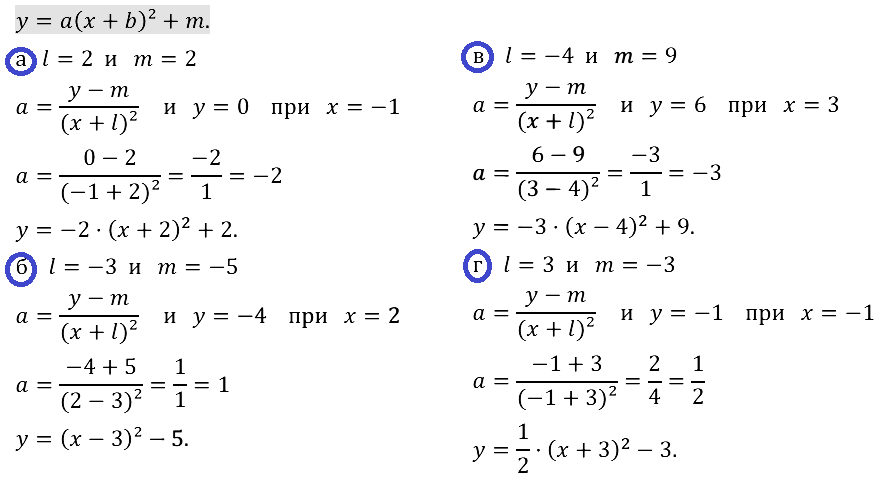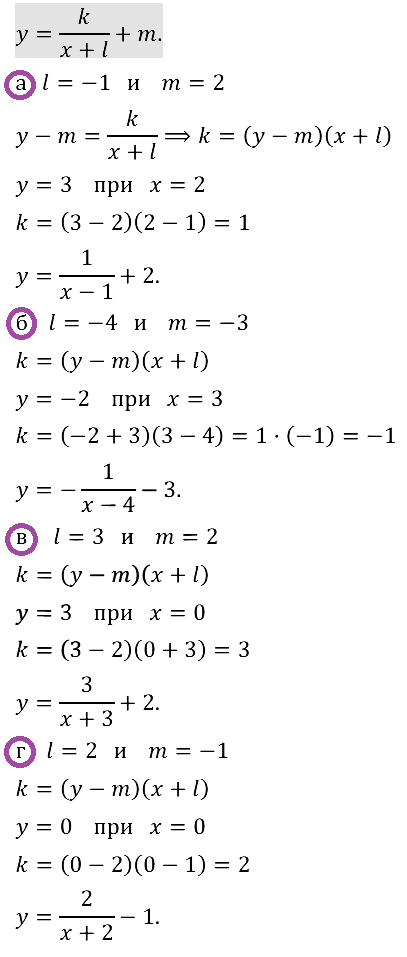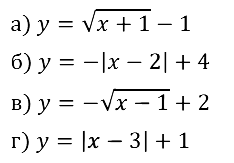Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 23. Как построить график функции y = f(x + l) + m, если известен график функции у = f(x). ОТВЕТЫ на упражнения 23.1 — 23.29. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 23.1 — 23.29)
§ 23. Как построить график функции y = f(x + l) + m,
если известен график функции у = f(x)
Постройте в одной системе координат графики функций:
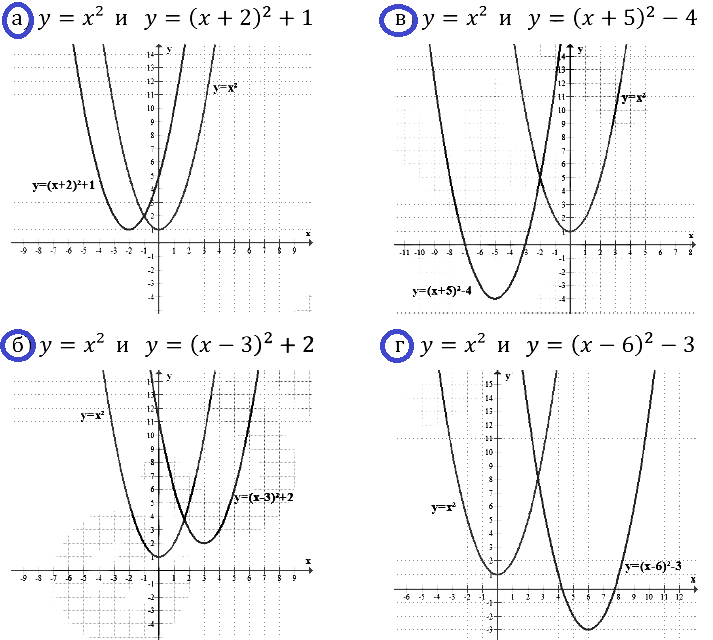
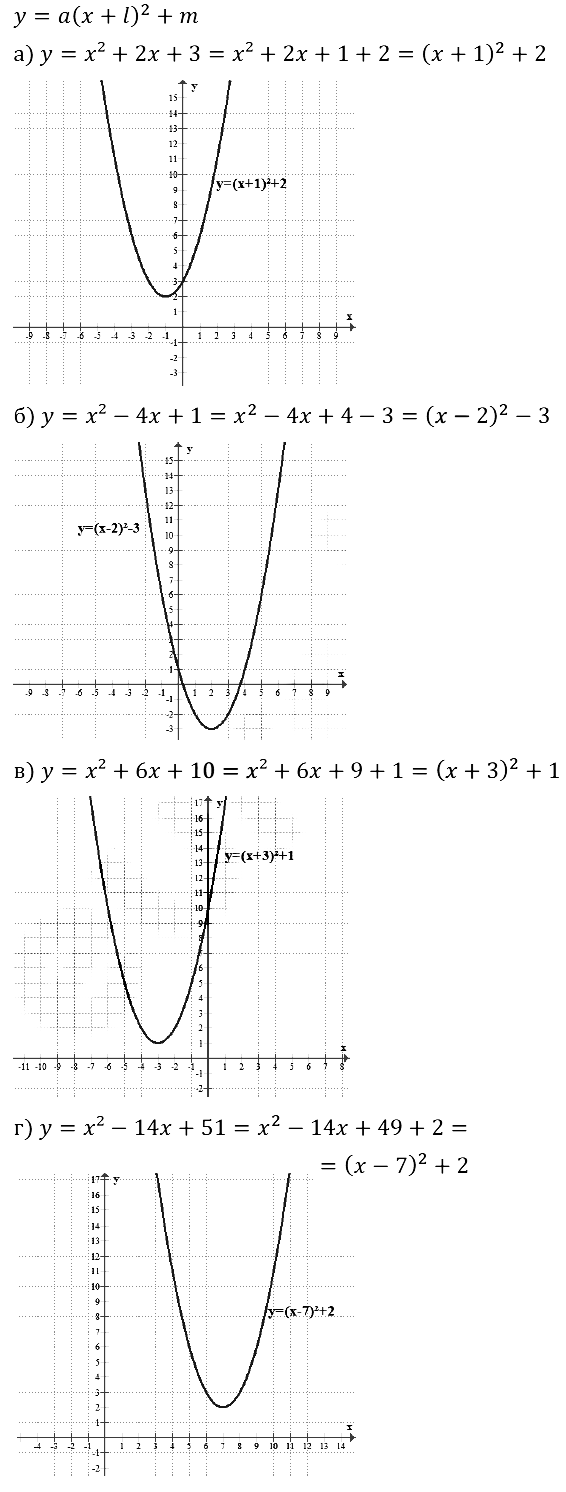
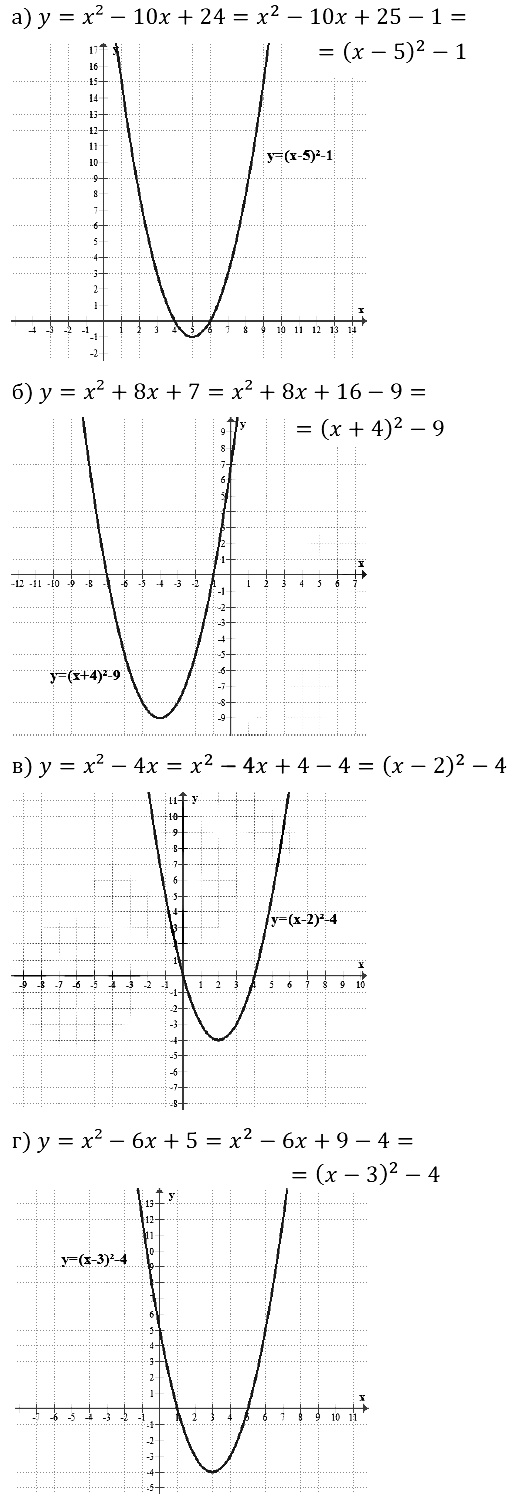
Задание № 23.1. а) у = х2 и у = (х + 2)2 + 1; б) у = х2 и у = (х – З)2 + 2; в) у = х2 и у = (x + 5)2 – 4; г) у = х2 и у = (х – 6)2 – 3.
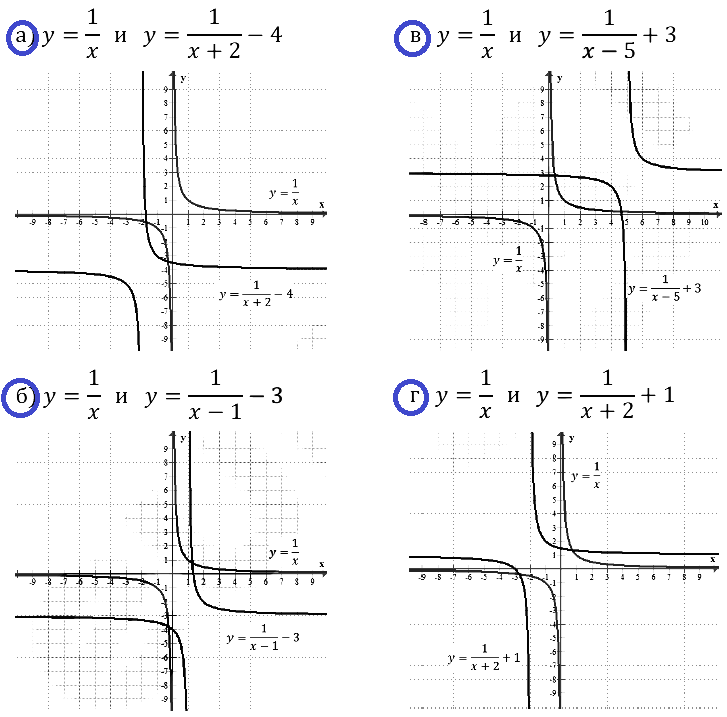
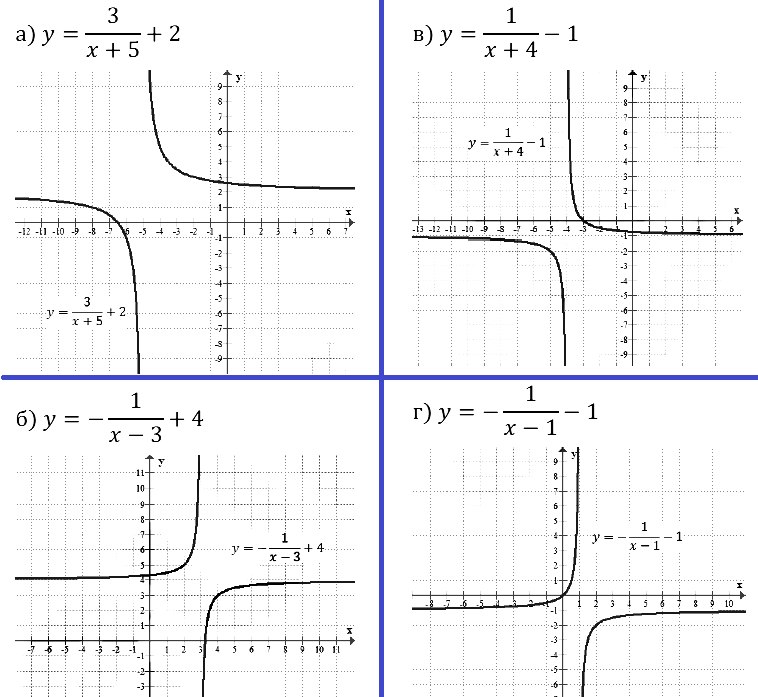
Задание № 23.2. а) у = 1/x и y = 1/(x+2) – 4; б) у = 1/x и y = 1/(x–1) – 3; в) у = 1/x и y = 1/(x–5) + 3; г) у = 1/x и y = 1/(x+2) + 1.
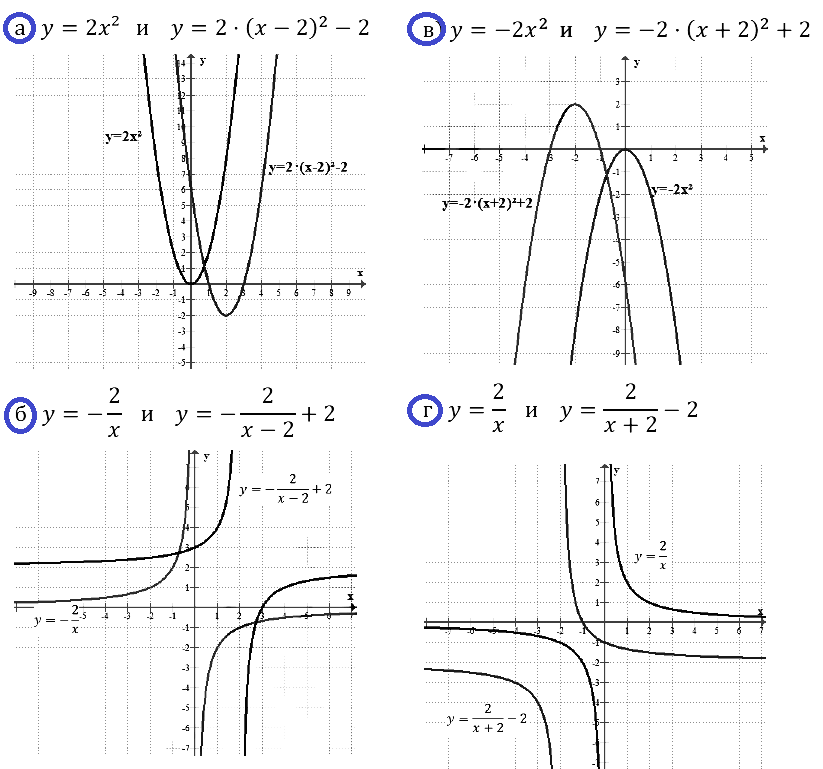
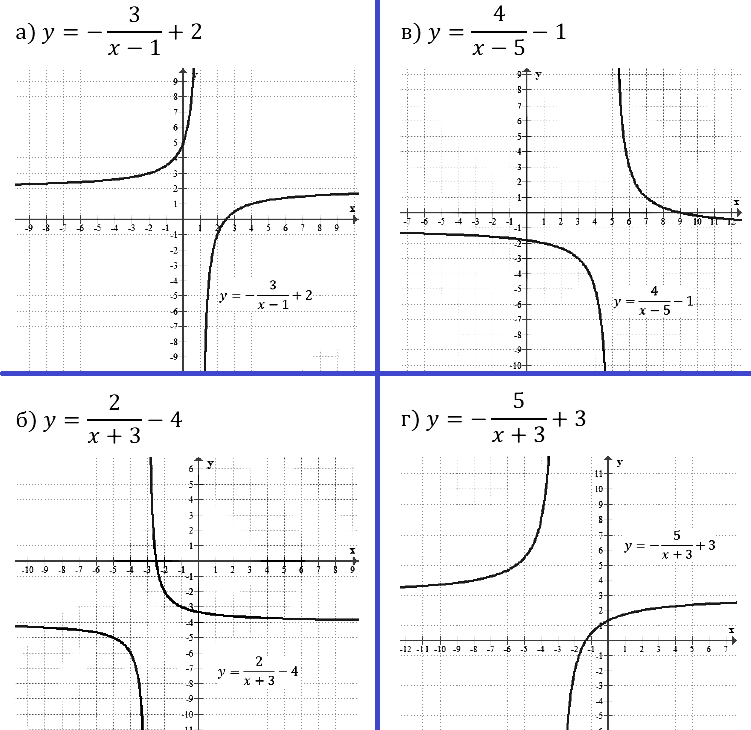
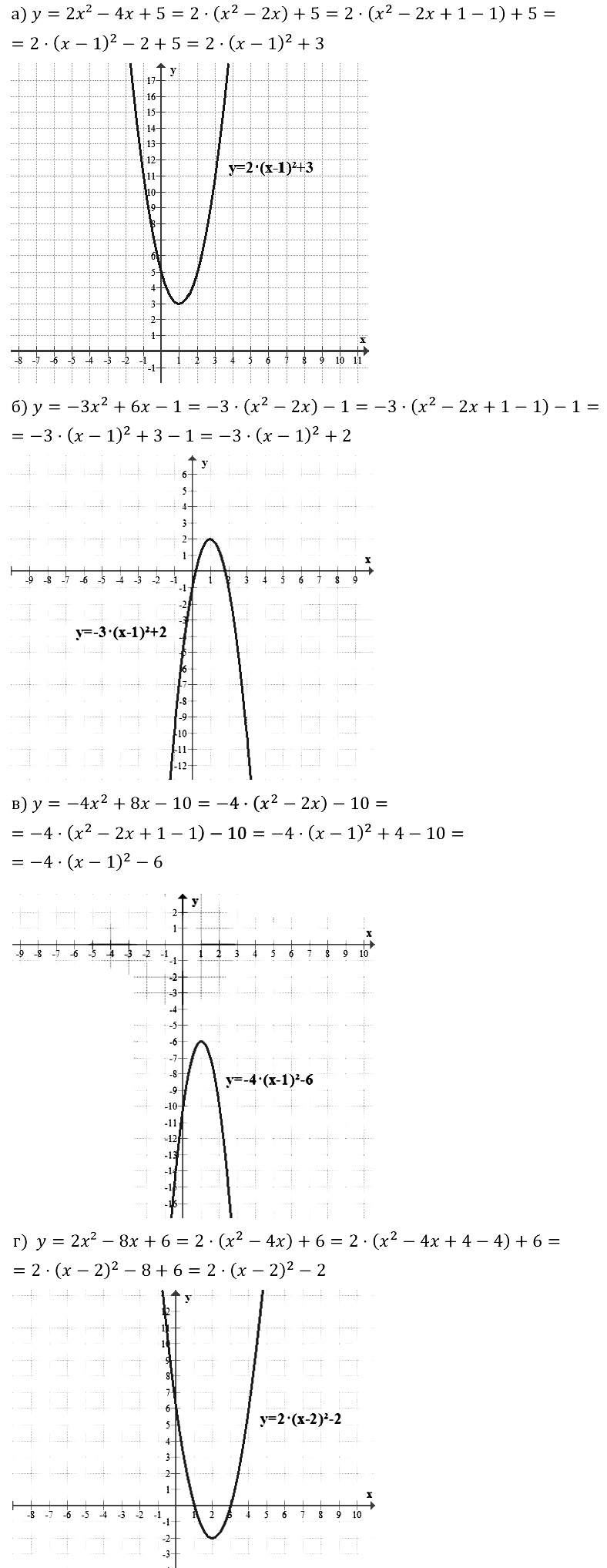
Задание № 23.3. а) у = 2х2 и у = 2(х – 2)2 – 2; б) у = –2/x и y = –2/(x–2) + 2; в) у = –2х2 и у = –2(х + 2)2 + 2; г) у = 2/x и у = 2/(x+2) – 2.
Задание № 23.4.
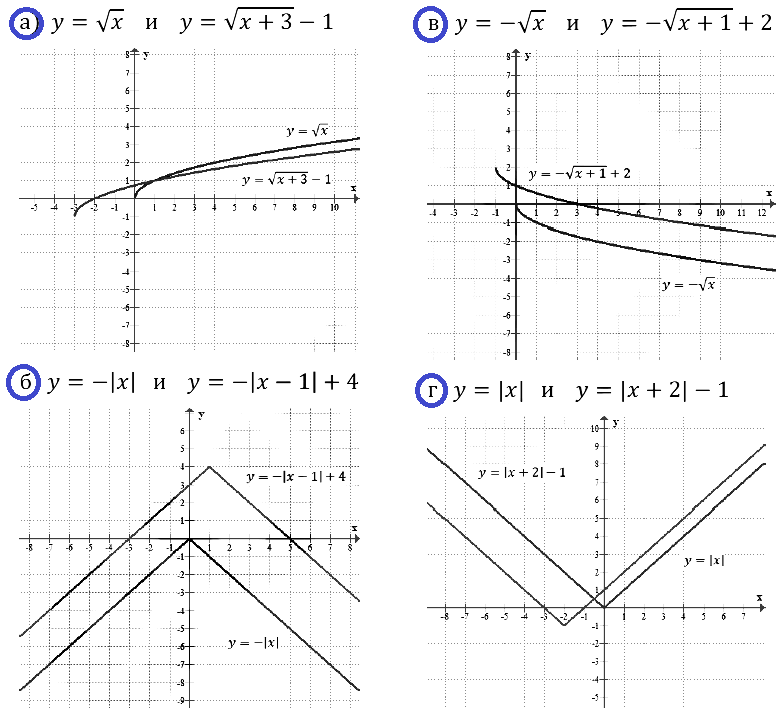
Задание № 23.5. График какой функции получится, если:
а) параболу у = 2,5x2 перенести на 3 единицы влево и на 4 единицы вниз;
б) гиперболу у = –4/x перенести на 2 единицы вправо и на 1 единицу вверх;
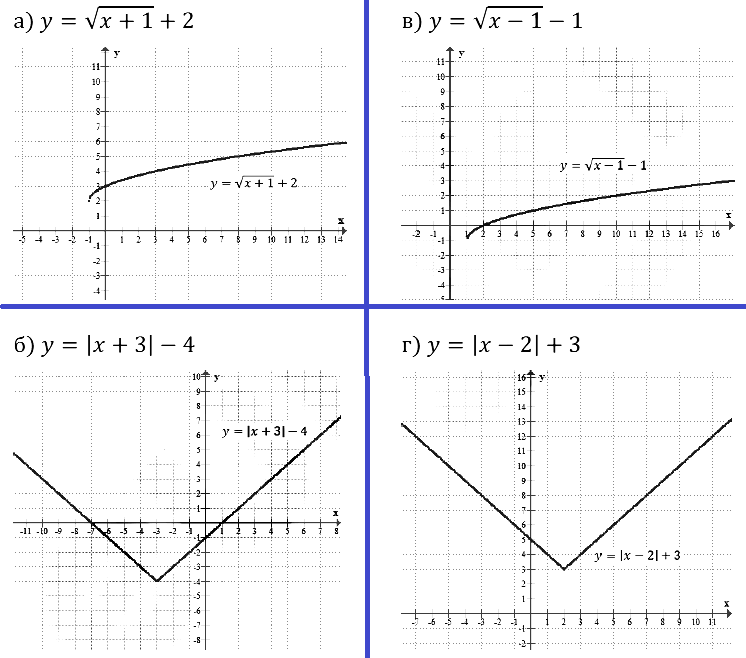
в) график функции у = √х перенести на 1 единицу влево и на 2 единицы вверх;
г) график функции у = |x| перенести на 3 единицы вправо и на 1 единицу вниз?
Задание № 23.6. График какой функции получится, если:
а) параболу у = –1/3 • х2 перенести на 2 единицы вправо и на 3 единицы вверх;
б) гиперболу у = 3/x перенести на 1 единицу влево и на 2 единицы вниз;
в) график функции у = –√х перенести на 4 единицы влево и на 2 единицы вниз;
г) график функции у = –|x| перенести на 6 единиц вправо и на 3 единицы вверх?
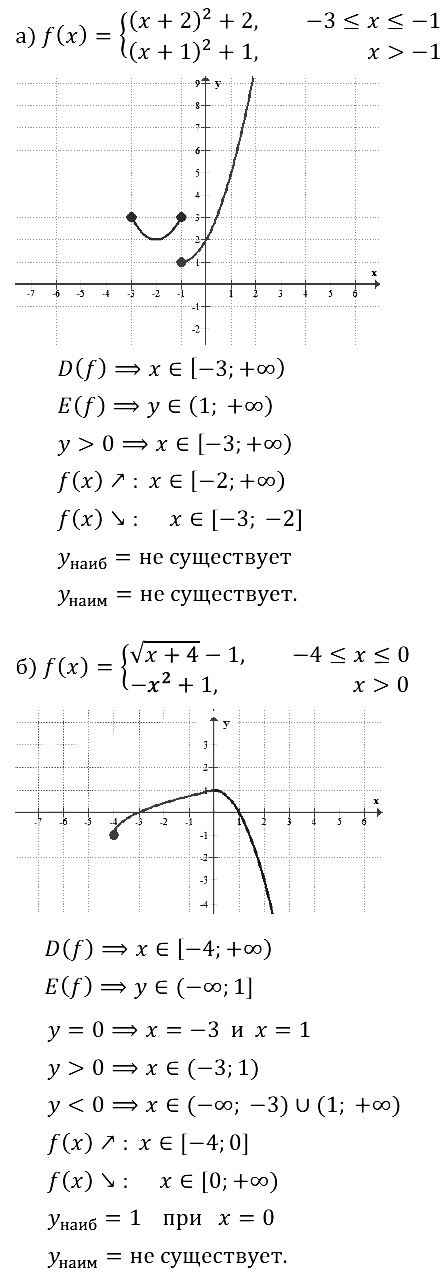
Задание № 23.7.
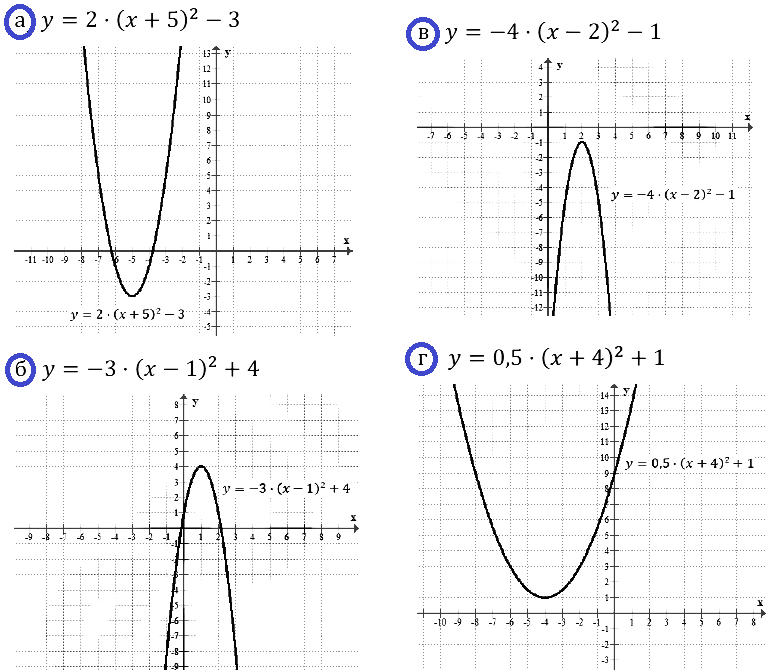
Задание № 23.8.
Задание № 23.9.
Задание № 23.10.
Задание № 23.11.
Задание № 23.12.
Задание № 23.13.
Задание № 23.14.
Задание № 23.15.
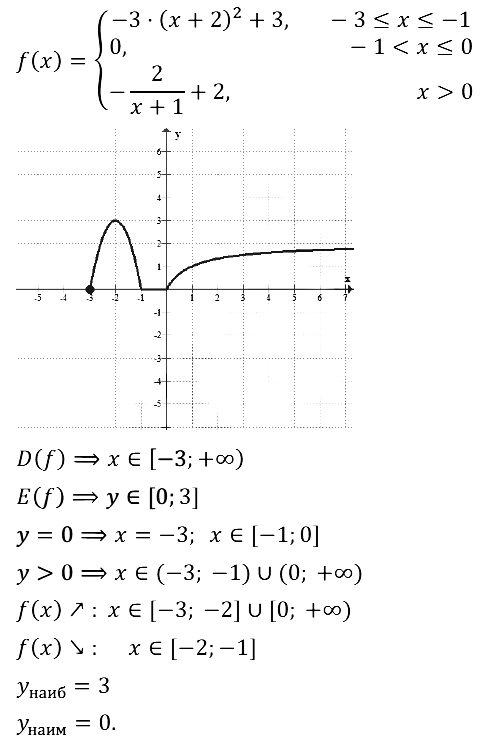
Задание № 23.16.
Задание № 23.17.
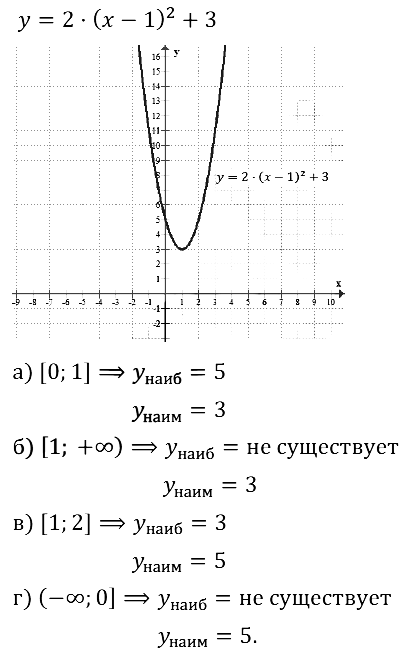
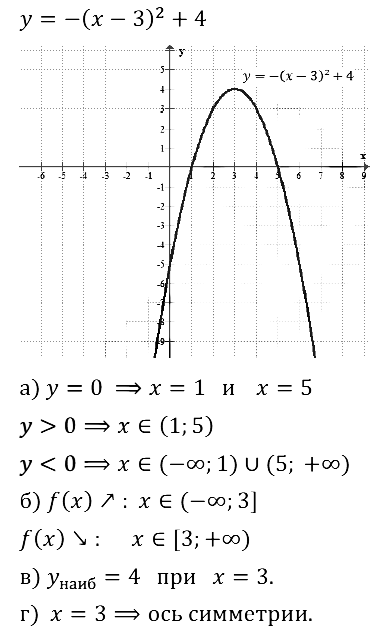
Задание № 23.18. Используя график функции у = –(х – 3)2 + 4:
а) найдите значения аргумента, при которых у = 0, у > 0, y < 0;
б) определите промежутки возрастания и убывания функции;
в) укажите наибольшее значение функции;
г) напишите уравнение оси симметрии параболы.
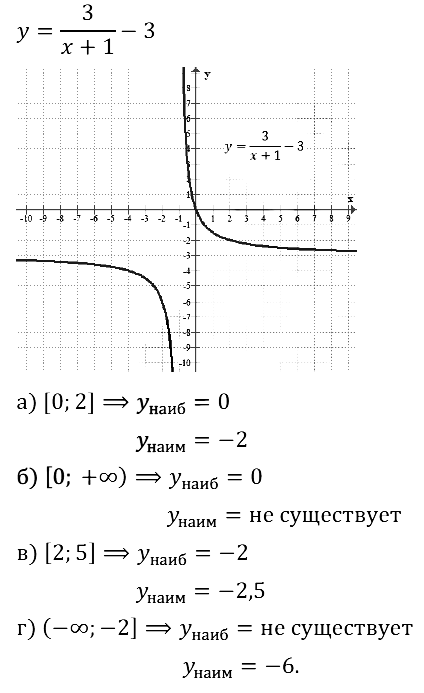
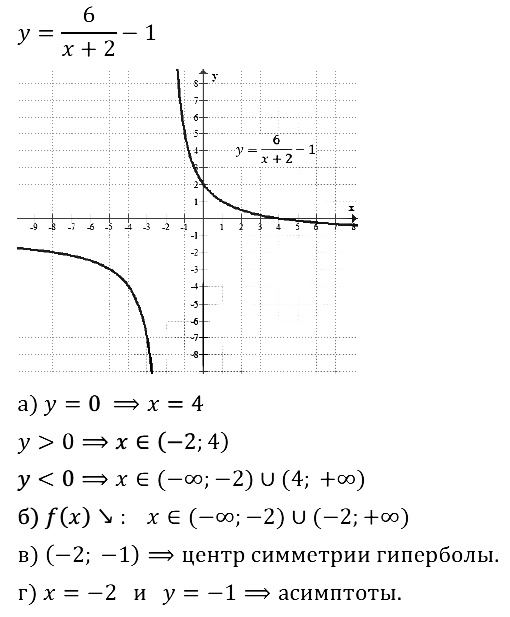
Задание № 23.19. Используя график функции у = 6/(x+2) – 1:
а) найдите значения аргумента, при которых у = 0, у > 0, y < 0;
б) определите промежутки убывания функции;
в) укажите центр симметрии гиперболы;
г) напишите уравнения асимптот гиперболы.
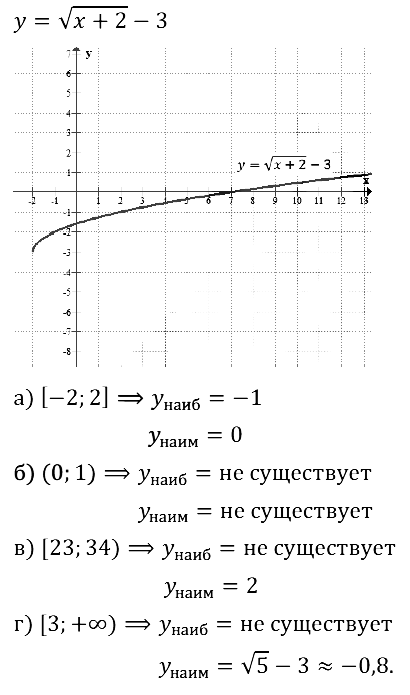
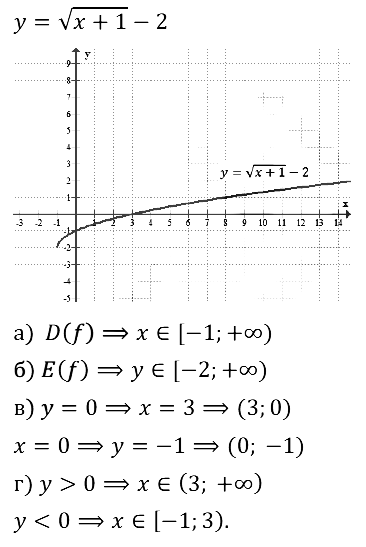
Задание № 23.20. Используя график функции у = √[x + 1] – 2, найдите:
а) область определения функции;
б) множество значений функции;
в) координаты точек пересечения графика с осями координат;
г) значения аргумента, при которых у > 0, у < 0.
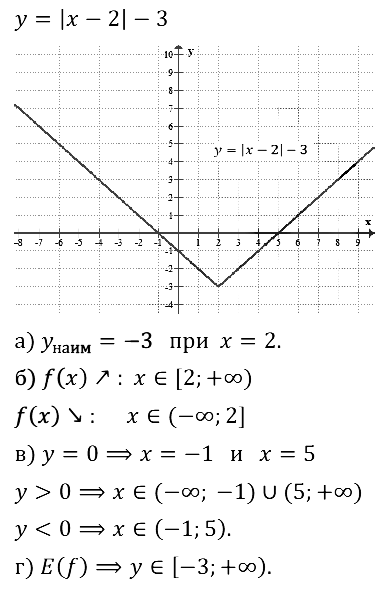
Задание № 23.21. Постройте график функции у = |х – 2| – 3. С помощью графика найдите:
а) наименьшее значение функции;
б) промежутки возрастания, убывания функции;
в) значения x, при которых у = 0, у > 0, у < 0;
г) множество значений функции.
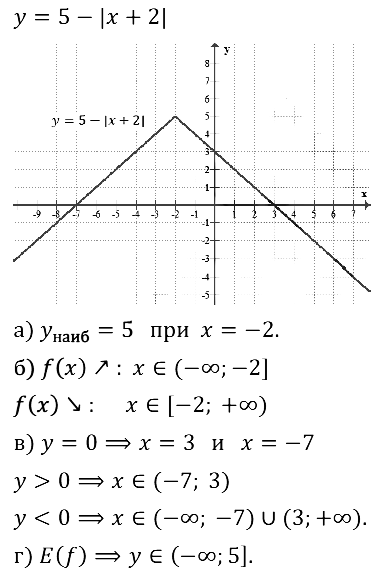
Задание № 23.22. Постройте график функции у = 5 – |х + 2|. С помощью графика найдите:
а) наибольшее значение функции;
б) промежутки возрастания, убывания функции;
в) значения x, при которых у = 0, у > 0, у < 0;
г) множество значений функции.
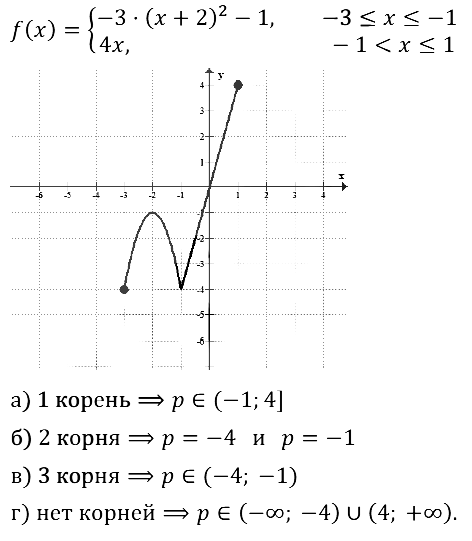
Задание № 23.23.
Задание № 23.24.
Задание № 23.25.
Задание № 23.26.
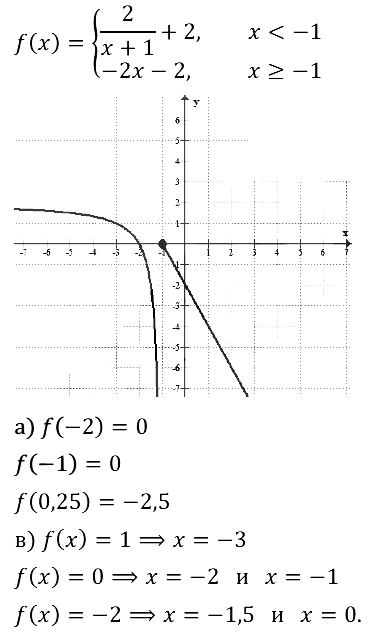
Задание № 23.27.
Задание № 23.28.
Задание № 23.29.
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 23. Как построить график функции y = f(x + l) + m, если известен график функции у = f(x). ОТВЕТЫ на упражнения 23.1 — 23.29. Вернуться в ОГЛАВЛЕНИЕ.