Упражнения: Центральные и вписанные углы

Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Центральные и вписанные углы». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.

Центральные и вписанные углы

Вариант 1

80. Чему равна градусная мера центрального угла окружности, опирающегося на дугу, составляющую 5/12 окружности?
81. Найдите градусные меры двух дуг окружности, на которые её делят две точки, если градусная мера одной из дуг на 100° больше градусной меры другой.
82. Найдите вписанный угол, если градусная мера дуги, на которую он опирается, равна: 1) 48°; 2) 254°; 3) 3α.
83. Точки В и D лежат на окружности по одну сторону от хорды АС. Найдите угол ADC, если ∠ABC = 42°.
84. Точка В окружности и её центр О лежат по разные стороны от хорды АС. Найдите: 1) угол АВС, если ∠AOС = 124°; 2) угол АОС, если ∠ABC = 94°.
85. Точки В и D лежат на окружности по разные стороны от хорды АС. Найдите угол ADC, если ∠ABC =78°.
86. Около треугольника АВС описана окружность с центром О. Найдите угол ВОС, если: 1) ∠A = 78°; 2) ∠А = 128°.
87. Точки А, В и С делят окружность на три дуги так, что ∪АВ : ∪ВС : ∪АС = 3 : 5 : 7. Найдите углы треугольника АВС.
88. Около треугольника АВС описана окружность с центром О. Найдите углы АОВ, ВОС и АОС, если 1) ∠A = 36°, ∠B = 78°; 2) ∠A = 23°, ∠B = 42°.
89. Найдите углы равнобедренного треугольника, вписанного в окружность, если основание этого треугольника стягивает дугу, градусная мера которой равна 192°.
90. Точка О — центр окружности, описанной около равнобедренного треугольника АВС (АС = ВС). Найдите углы треугольника АВС, если ∠AOB = 128°. Сколько решений имеет задача?
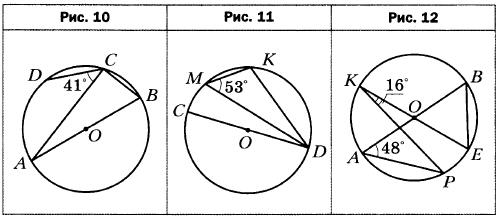
91. Точки С и D окружности лежат по одну сторону от диаметра АВ (рис. 10). Найдите угол DCB, если ∠ACD = 41°.
92. Точки М и К окружности лежат по одну сторону от диаметра CD (рис. 11). Найдите угол CDK, если ∠DMK = 53°.
93. Две окружности пересекаются в точках С и D. Через точку С проведены диаметры СЛ и СВ. Найдите углы САВ и СВА, если ∠ACD = 55°, ∠BCD = 70°.
94. В окружности с центром О проведены диаметры АВ и КЕ (рис. 12). Найдите угол АВЕ, если ∠PKE = 16°, ∠BAP = 48°.
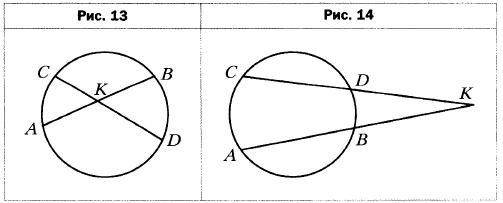
95. Хорды АВ и CD окружности пересекаются в точке К (рис. 13). Найдите угол АКС, если ∪АС = 36°, ∪BD = 42°.
96. Хорды АВ и CD окружности не пересекаются, а прямые АВ и CD пересекаются в точке К (рис. 14). Найдите угол АКС, если ∪АС = 84°, ∪BD = 28°.
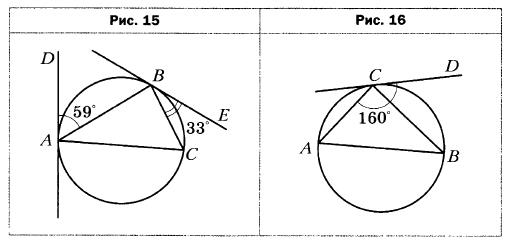
97. Прямые AD и BE касаются окружности, описанной около треугольника АВС, в точках А и В соответственно (рис. 15). Найдите углы треугольника АВС, если ∠BAD = 59°, ∠CBE = 33°.
98. Через точку С окружности проведена касательная CD, не параллельная диаметру АВ (рис. 16). Найдите углы треугольника АВС, если ∠DCA = 160°.
99. Угол при вершине равнобедренного треугольника равен 78°. На боковой стороне треугольника как на диаметре построена полуокружность, которую другие стороны треугольника делят на три дуги. Найдите градусные меры образовавшихся дуг.

Вариант 2

80. Чему равна градусная мера центрального угла окружности, опирающегося на дугу, составляющую 5/18 окружности?
81. Найдите градусные меры двух дуг окружности, на которые её делят две точки, если градусная мера одной из дуг на 80° больше градусной меры другой.
82. Найдите вписанный угол, если градусная мера дуги, на которую он опирается, равна: 1) 32°; 2) 328°; 3) 2β.
83. Точки К и D лежат на окружности по одну сторону от хорды АВ. Найдите угол АКВ, если ∠ADB = 129°.
84. Точка А окружности и её центр О лежат по разные стороны от хорды MN. Найдите: 1) угол MAN, если ∠MON = 136°; 2) угол MON, если ∠MAN = 129°.
85. Точки К и D лежат на окружности по разные стороны от хорды А В. Найдите угол ADB, если ∠AKB = 107°.
86. Около треугольника DEF описана окружность с центром О. Найдите угол DOF, если: 1) ∠E = 38°; 2) ∠E = 148°.
87. Точки В, С и D делят окружность на три дуги так, что ∪BC : ∪CD : ∪BD = 3 : 4 : 5. Найдите углы треугольника BCD.
88. Около треугольника АВС описана окружность с центром О. Найдите углы АОВ, ВОС и АОС, если 1) ∠A = 48°, ∠C = 63°; 2) ∠A = 37°, ∠C = 44°.
89. Найдите углы равнобедренного треугольника, вписанного в окружность, если боковая сторона этого треугольника стягивает дугу, градусная мера которой равна 38°.
90. Точка О — центр окружности, описанной около равнобедренного треугольника DEF (DF = EF). Найдите углы треугольника DEF, если ∠DOE = 116°. Сколько решений имеет задача?
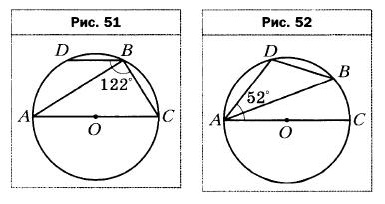
91. Точки D и В окружности лежат по одну сторону от диаметра АС (рис. 51). Найдите угол ABD, если ∠DBC = 122°.
92. Точки D и В окружности лежат по одну сторону от диаметра АС (рис. 52). Найдите угол ABD, если ∠DAC = 52°.
93. Две окружности пересекаются в точках Е и F. Через точку Е проведены диаметры ED и ЕК. Найдите углы DEF и KEF, если ∠EDF = 35°, ∠EKF = 50°.
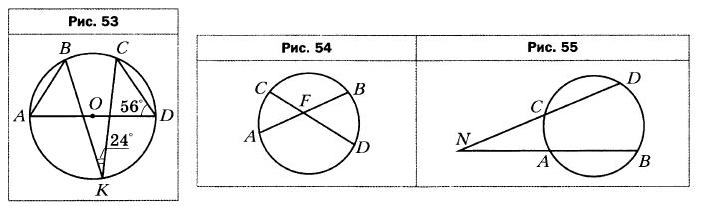
94. В окружности с центром О проведён диаметр AD (рис. 53). Найдите угол BAD, если ∠CDA = 56°, ∠BKC = 24°.
95. Хорды АВ и CD окружности пересекаются в точке F (рис. 54). Найдите угол AFD, если ∪AD = 142°, ∪ВС = 116°.
96. Хорды АВ и CD окружности не пересекаются, а прямые АВ и CD пересекаются в точке N (рис. 55). Найдите угол BND, если ∪AC = 24°, ∠BD =72°.
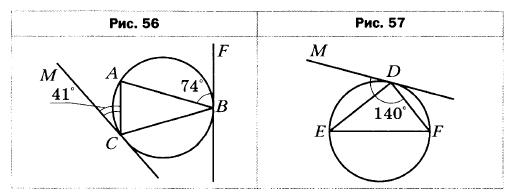
97. Прямые BF и СМ касаются окружности, описанной около треугольника АВ С, в точках В и С соответственно (рис. 56). Найдите углы треугольника АВС, если ∠ABF = 74°, ∠ACM= 41°.
98. Через точку D окружности проведена касательная DM, не параллельная диаметру EF (рис. 57). Найдите углы треугольника DEF, если ∠MDF = 140°.
99. Угол при вершине равнобедренного треугольника равен 86°. На основании треугольника как на диаметре построена полуокружность, которую другие стороны треугольника делят на три дуги. Найдите градусные меры образовавшихся дуг.

Вариант 3

80. Чему равна градусная мера центрального угла окружности, опирающегося на дугу, составляющую 3/8 окружности?
81. Найдите градусные меры двух дуг окружности, на которые её делят две точки, если градусная мера одной из дуг на 140° меньше градусной меры другой.
82. Найдите вписанный угол, если градусная мера дуги, на которую он опирается, равна: 1) 38°; 2) 226°; 3) γ/2.
83. Точки М и N лежат на окружности по одну сторону от хорды АВ. Найдите угол ANB, если ∠AMB = 63°.
84. Точка М окружности и её центр О лежат по разные стороны от хорды АВ. Найдите: 1) угол AMВ, если ∠AOB = 152°; 2) угол АОВ, если ∠AMB = 73°.
85. Точки М и N лежат на окружности по разные стороны от хорды АВ. Найдите угол АМВ, если ∠ANB = 82°.
86. Около треугольника АВС описана окружность с центром О. Найдите угол АОВ, если: 1) ∠C = 54°; 2) ∠C = 136°.
87. Точки D, Е и F делят окружность на три дуги так, что ∪DE : ∪EF : ∪DF = 2 : 9 : 7. Найдите углы треугольника DEF.
88. Около треугольника АВС описана окружность с центром О. Найдите углы АОВ, ВОС и АОС, если 1) ∠B = 52°, ∠C= 64°; 2) ∠B = 17°, ∠C = 68°.
89. Найдите углы равнобедренного треугольника, вписанного в окружность, если основание этого треугольника стягивает дугу, градусная мера которой равна 100°.
90. Точка О — центр окружности, описанной около равнобедренного треугольника АВС (АВ = АС). Найдите углы треугольника АВС, если ∠BOC = 32°. Сколько решений имеет задача?
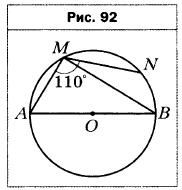
91. Точки М и N окружности лежат по одну сторону от диаметра АВ (рис. 92). Найдите угол BMN, если ∠AMN = 110°.
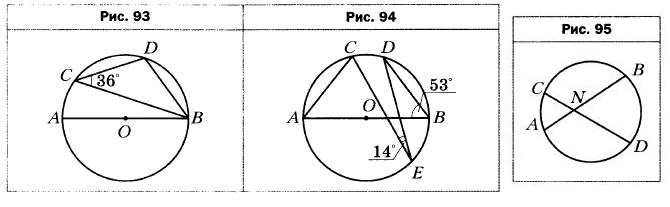
92. Точки С и D окружности лежат по одну сторону от диаметра АВ (рис. 93). Найдите угол ABD, если ∠BCD = 36°.
93. Две окружности пересекаются в точках А и В. Через точку А проведены диаметры АС и AD. Найдите углы АСВ и BAD, если ∠BAC = 65°, ∠ADB = 40°.
94. В окружности с центром О проведён диаметр АВ (рис. 94). Найдите угол САВ, если ∠CED = 14°, ∠ABD = 53°.
95. Хорды АВ и CD окружности пересекаются в точке N (рис. 95). Найдите угол BND, если ∪АС = 44°, ∪BD = 96°.
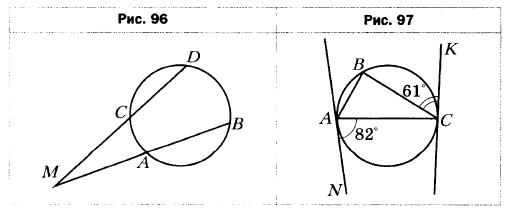
96. Хорды АВ и CD окружности не пересекаются, а прямые А В и CD пересекаются в точке М (рис. 96). Найдите угол DMB, если ∪АС = 38°, ∪BD= 116°.
97. Прямые AN и СК касаются окружности, описанной около треугольника АВС, в точках А и С соответственно (рис. 97). Найдите углы треугольника АВС, если ∠CAN = 82°, ∠BCK = 61°.
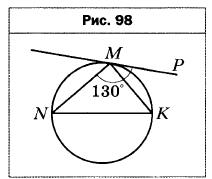
98. Через точку М окружности проведена касательная МР, не параллельная диаметру NK (рис. 98). Найдите углы треугольника MNK, если ∠PMN = 130°.
99. Угол при вершине равнобедренного треугольника равен 62°. На боковой стороне треугольника как на диаметре построена полуокружность, которую другие стороны треугольника делят на три дуги. Найдите градусные меры образовавшихся дуг.

Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Трапеция». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки! 

Вернуться к Списку упражнений по геометрии УМК Мерзляк