Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Подобные треугольники». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Подобные треугольники
Вариант 1
- Известно, что ΔАВС ∼ ΔА1В1С1, причём стороне АВ соответствует сторона А1В1, а стороне ВС — сторона В1С1 (рис. 21). Найдите неизвестные стороны этих треугольников (размеры сторон даны в сантиметрах).
- Стороны треугольника относятся как 7 : 6 : 3. Найдите стороны подобного ему треугольника, если:
1) его периметр равен 8 см; 2) его наименьшая сторона равна 6 см; 3) разность его наибольшей и наименьшей сторон равна 20 см. - Известно, что
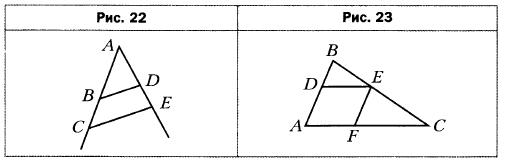
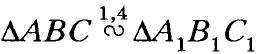 , причём ∠A = ∠A1, ∠B = ∠B1. Найдите стороны треугольников АВС и А1В1С1, если АВ + А1В1 = 36 см и АВ : ВС : АС = 3 : 7 : 8.
, причём ∠A = ∠A1, ∠B = ∠B1. Найдите стороны треугольников АВС и А1В1С1, если АВ + А1В1 = 36 см и АВ : ВС : АС = 3 : 7 : 8. - Найдите подобные треугольники на рисунке 22, если известно, что BD II СЕ. Запишите пропорции, начинающиеся с отношения: 1) AC / CE, 2) BD / CE.
- Продолжения боковых сторон АВ и CD трапеции ABCD пересекаются в точке Е. Большее основание AD трапеции равно 12 см, АЕ = 15 см, BE = 5 см. Найдите меньшее основание трапеции.
- В треугольник АВС вписан параллелограмм ADEF (рис. 23). Найдите сторону АС треугольника, если АВ = 20 см, FE = 12 см, AF = 14 см.
- В треугольник АВС вписан ромб АКРЕ так, что угол А у них общий, а вершина Р принадлежит стороне ВС. Найдите сторону ромба, если АВ = 6 см, АС = 3 см.
- Сторона треугольника равна 12 см, а высота, проведённая к ней, — 4 см. В треугольник вписан прямоугольник, большая сторона которого принадлежит данной стороне треугольника. Найдите стороны прямоугольника, если они относятся как 5 : 9.
Вариант 2
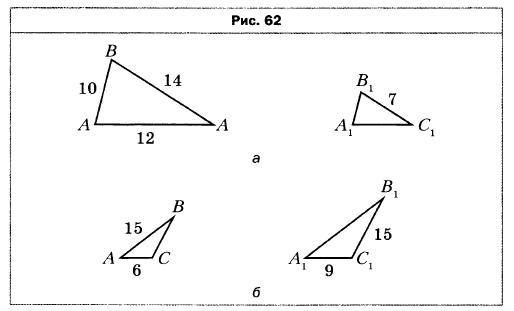
- Известно, что ΔABС ∼ ΔA1B1C1, причём стороне АВ соответствует сторона A1B1, а стороне ВС — сторона В1С1 (рис. 62). Найдите неизвестные стороны этих треугольников (размеры сторон даны в сантиметрах).
- Стороны треугольника относятся как 5 : 11 : 14. Найдите стороны подобного ему треугольника, если:
1) его периметр равен 120 см; 2) его средняя по длине сторона равна 55 см; 3) сумма его наибольшей и средней по длине сторон равна 50 см. - Известно, что
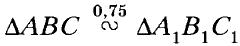 , причём ∠A = ∠A1, ∠C = ∠C1. Найдите стороны треугольников АВС и A1B1C1, если АС + А1С1 = 112 см и А1В1 : В1С1 : A1С1 = 4 : 5 : 8.
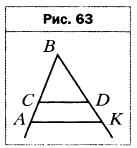
, причём ∠A = ∠A1, ∠C = ∠C1. Найдите стороны треугольников АВС и A1B1C1, если АС + А1С1 = 112 см и А1В1 : В1С1 : A1С1 = 4 : 5 : 8. - Найдите подобные треугольники на рисунке 63, если известно, что CD II АК. Запишите пропорции, начинающиеся с отношения: 1) ВС / BА, 2) АK / CD.
- Продолжения боковых сторон АВ и CD трапеции ABCD пересекаются в точке К. Меньшее основание ВС трапеции равно 4 см, КВ = 5 см, АВ = 7 см. Найдите большее основание трапеции.
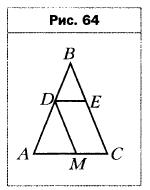
- В треугольник АВС вписан параллелограмм DECM (рис. 64). Найдите сторону ВС треугольника, если АС = 10 см, МС = 4 см, DM = 9 см.
- В треугольник АВС вписан ромб CDKF так, что угол С у них общий, а вершина К принадлежит стороне АВ. Найдите сторону АС треугольника, если сторона ромба равна 4 см и BF = 3 см.
- В треугольник со стороной 12 см вписан прямоугольник, стороны которого равны 8 см и 5 см. Большая сторона прямоугольника принадлежит данной стороне треугольника. Найдите высоту треугольника, проведённую к данной стороне.
Вариант 3
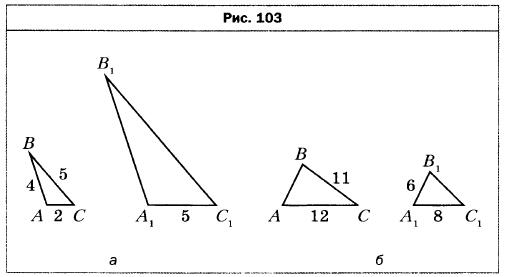
- Известно, что ΔАВС ∼ ΔА1В1С1, причём стороне АВ соответствует сторона A1B1, а стороне ВС — сторона В1С1 (рис. 103). Найдите неизвестные стороны этих треугольников (размеры сторон даны в сантиметрах).
- Стороны треугольника относятся как 7 : 5 : 9. Найдите стороны подобного ему треугольника, если:
1) его периметр равен 42 см; 2) его наибольшая сторона равна 27 см; 3) сумма его наибольшей и наименьшей сторон равна 84 см. - Известно, что
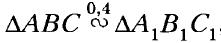 , причём ∠B = ∠B1, ∠C = ∠C1. Найдите стороны треугольников АВС и А1В1С1, если АС + А1С1 = 56 см и АВ : ВС : АС = 2 : 3 : 4.
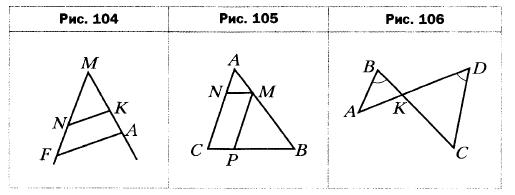
, причём ∠B = ∠B1, ∠C = ∠C1. Найдите стороны треугольников АВС и А1В1С1, если АС + А1С1 = 56 см и АВ : ВС : АС = 2 : 3 : 4. - Найдите подобные треугольники на рисунке 104, если известно, что NK II FA. Запишите пропорции, начинающиеся с отношения: 1) MK / MN; 2) MF / MN.
- Продолжения боковых сторон АВ и CD трапеции ABCD пересекаются в точке М. Большее основание AD трапеции равно 26 см, МС = 9 см, CD = 4 см. Найдите меньшее основание трапеции.
- В треугольник АВС вписан параллелограмм MNCP (рис. 105). Найдите сторону МР параллелограмма, если АС = 10 см, ВС = 12 см, PC = 3 см.
- В треугольник АВС вписан ромб BDEF так, что угол В у них общий, а вершина Е принадлежит стороне АС. Найдите сторону ромба, если АВ = 12см, ВС = 6см.
- Сторона треугольника равна 10 см, а высота, проведённая к ней, — 7 см. В треугольник вписан прямоугольник, меньшая сторона которого принадлежит данной стороне треугольника. Найдите стороны прямоугольника, если они относятся как 4 : 7.
Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Подобные треугольники». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!