Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Теорема Фалеса. Теорема о пропорциональных отрезках». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Теорема Фалеса.
Теорема о пропорциональных отрезках
Вариант 1
- Начертите произвольный отрезок MN и постройте на нём точку К такую, что МК : KN = 2 : 3.
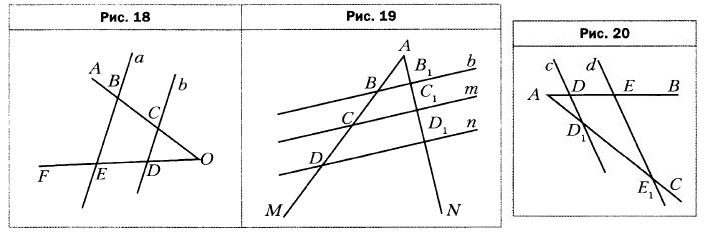
- Параллельные прямые а и b пересекают стороны угла AOF (рис. 18). Найдите отрезок OD, если ОС = 4 см, ВС = 6 см, DE = 9 см.
- Параллельные прямые b, m и n пересекают стороны угла MAN (рис. 19). Найдите отрезки АВ1 и BD, если АВ = 4 см, CD = 8 см, В1С1 = 5 см, C1D1 = 6 см.
- Параллельные прямые c и d пересекают стороны угла ВАС (рис. 20). Найдите отрезок DE, если AD = 4 см, D1E1 = 16 см и DE = AD1.
- В прямоугольном треугольнике ABC ∠C = 90°, ∠A = 30°, АС = 16 см. Точка М — середина катета ВС. Найдите расстояние от точки М до гипотенузы АВ.
- В треугольнике АВС АВ = 6 см, ВС = 8 см. Через середину стороны АС проведены прямые, параллельные сторонам АВ и ВС. Найдите периметр образовавшегося четырёхугольника.
- Через точку Е — середину боковой стороны АВ трапеции ABCD — проведена прямая, параллельная стороне CD и пересекающая основание AD в точке F. Найдите сторону CD, если EF = 10 см.
- В окружности проведены хорды АВ и АС. Расстояние от середины хорды АС до хорды АВ равно 4 см. Найдите длину отрезка ВС, если ∠ABC = 30°.
- Диагональ трапеции делит её среднюю линию на отрезки, один из которых на 5 см больше другого. Найдите большее основание трапеции, если её меньшее основание равно 6 см.
- Основания трапеции равны 8 см и 12 см. Диагонали трапеции пересекают её среднюю линию в точках М и К. Найдите отрезок МК.
- Основания трапеции равны 10 см и 6 см. Боковую сторону трапеции разделили на 4 равных отрезка и через точки деления провели прямые, параллельные основаниям. Найдите отрезки этих прямых, принадлежащие трапеции.
- Сторону ВС треугольника АВС разделили на 3 равных отрезка и через точки деления провели прямые, параллельные стороне АВ. Найдите отрезки этих прямых, принадлежащие треугольнику АВС, если АВ = 12 см.
- В равнобедренном треугольнике АВС (АВ = ВС) точка М пересечения медиан удалена от основания на 4 см. Найдите расстояние от точки М до вершины В.
- Медианы прямоугольного треугольника ABC (∠C = 90°) пересекаются в точке М. Найдите гипотенузу АВ, если СМ = 6 см.
- В равнобедренном треугольнике АВС (АВ = ВС) середина боковой стороны удалена от основания на 6 см. Найдите расстояние от точки пересечения медиан треугольника АВС до вершины В.
- Отрезок BD — биссектриса треугольника АВС. Найдите: 1) отрезки AD и DC, если АВ = 8 см, ВС = 14 см, АС = 11 см; 2) сторону ВС, если AD : DC = 2 : 3, АВ = 18 см; 3) стороны АВ и ВС, если АВ + ВС = 56 см, AD = 9 см, DC = 15 см.
- Стороны треугольника равны 13 см, 18 см и 21 см. Окружность, центр которой принадлежит меньшей стороне треугольника, касается двух других сторон. Найдите отрезки, на которые центр окружности делит сторону треугольника.
- В треугольнике АВС АВ = 7 см, ВС = 15 см, АС =11 см. В каком отношении центр окружности, вписанной в треугольник, делит его биссектрису BD?
- На медиане AD треугольника АВС отметили точку F так, что AF: FD = 7 : 4. В каком отношении прямая BF делит сторону АС?
- На сторонах АВ и ВС треугольника АВС отметили точки Е и D соответственно. Отрезки AD и СЕ пересекаются в точке F. В каком отношении точка F делит отрезок СЕ, если BE : ЕА = 2 : 1 и BD : DC = 6 : 7?
Вариант 2
- Начертите произвольный отрезок АВ и постройте на нём точку С такую, что АС : СВ = 3 : 4.
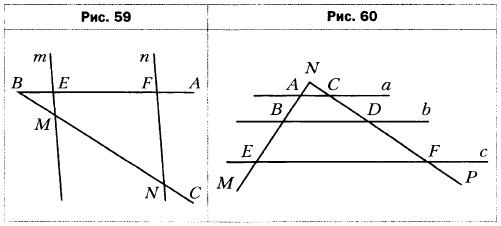
- Параллельные прямые тип пересекают стороны угла АВС (рис. 59). Найдите отрезок MN, если BE = 4 см, ЕЕ = 12 см, ВМ = 5 см.
- Параллельные прямые а, b и с пересекают стороны угла MNP (рис. 60). Найдите отрезки BE и CF, если AN = 2 см, NC = 3 см, DF = 9 см, АВ = 4 см.
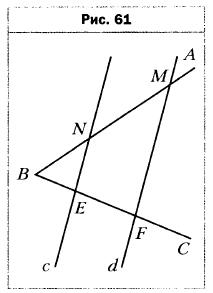
- Параллельные прямые с и d пересекают стороны угла АВС (рис. 61). Найдите отрезок EF, если BE = 4 см, MN = 9 см, BN = EF.
- В прямоугольном треугольнике АВС известно, что ∠C = 90°, ∠B = 60°, АС = 24 см. Точка К — середина катета АС. Найдите расстояние от точки К до гипотенузы АВ.
- В треугольнике АВС известно, что АС = 10 см, ВС = 4 см. Через середину стороны АВ проведены прямые, параллельные сторонам АС к ВС. Найдите периметр образовавшегося четырёхугольника.
- Через точку К — середину боковой стороны CD трапеции ABCD — проведена прямая, параллельная стороне АВ и пересекающая основание AD в точке Р. Найдите отрезок КР, если АВ = 14 см.
- В окружности проведены хорды ВА и ВС. Расстояние от середины хорды ВС до хорды ВА равно 5 см. Найдите угол САВ, если АС = 20 см.
- Диагональ трапеции делит её среднюю линию на отрезки, один из которых на 3 см меньше другого. Найдите меньшее основание трапеции, если её большее основание равно 14 см.
- Меньшее основание трапеции равно 6 см. Диагонали трапеции пересекают её среднюю линию в точках М и N. Найдите большее основание трапеции, если MN = 4 см.
- Боковую сторону трапеции разделили на 4 равных отрезка и через точки деления провели прямые, параллельные основаниям. Два меньших отрезка этих прямых, принадлежащие трапеции, равны 4 см и 7 см. Найдите основания трапеции.
- Сторону АВ треугольника АВС разделили на 3 равных отрезка и через точки деления провели прямые, параллельные стороне ВС. Найдите отрезки этих прямых, принадлежащие треугольнику AВС, если наименьший из этих отрезков на 6 см меньше стороны ВС.
- В равнобедренном треугольнике AВС (AС = ВС) точка М пересечения медиан удалена от вершины С на 10 см. Найдите расстояние от точки М до основания.
- В прямоугольном треугольнике AВС (∠C = 90°) медианы пересекаются в точке М, точка О — середина AВ. Найдите гипотенузу AВ, если ОМ = 4 см.
- В равнобедренном треугольнике AВС (AВ = ВС) точка пересечения медиан удалена от вершины В на 4 см. Найдите расстояние от середины боковой стороны треугольника AВС до его основания.
- Отрезок AК — биссектриса треугольника AВС. Найдите:
1) отрезки ВК и КС, если AB = 8 см, AC = 12 см, ВС = 10 см;
2) сторону AB, если ВК : КС = 3 : 7, AC = 28 см;
3) стороны AB и AC, если AC – AB = 9 см, ВК : КС = 4 : 7.
- Стороны треугольника равны 15 см, 18 см и 22 см. Окружность, центр которой принадлежит большей стороне треугольника, касается двух других сторон. Найдите отрезки, на которые центр окружности делит сторону треугольника.
- В треугольнике ABС AB = 10 см, ВС = 9 см, AC =17 см. В каком отношении центр окружности, вписанной в треугольник, делит его биссектрису AM?
- На медиане AD треугольника ABС отметили точку М так, что AM : MD = 5 : 3. В каком отношении прямая ВМ делит сторону AC?
- На сторонах AC и ВС треугольника ABС отметили точки Е и F соответственно. Отрезки AF и BE пересекаются в точке К. В каком отношении точка К делит отрезок BE, если AЕ : ЕС = 1 : 3 и BF : FC = 3 : 8?
Вариант 3
- Начертите произвольный отрезок CD и постройте на нём точку Е такую, что СЕ : ED = 5 : 2.
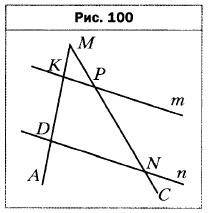
- Параллельные прямые m и n пересекают стороны угла АМС (рис. 100). Найдите отрезок PN, если МК = 2 см, KD = 4 см, МР = 3 см.
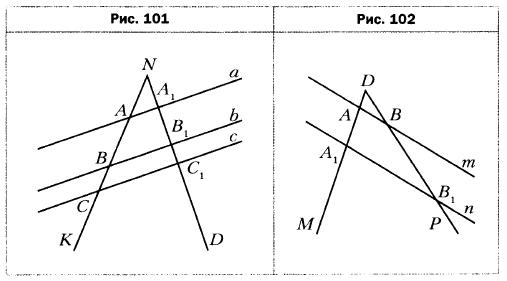
- Параллельные прямые а, b и с пересекают стороны угла KND (рис. 101). Найдите отрезки NA и АС, если NA1 = 5 см, АВ = 8 см, А1В1 = 6 см, В1С1 = 3 см.
- Параллельные прямые тип пересекают стороны угла MDP (рис. 102). Найдите отрезок AA1 если DA = 8 см, ВВ1 = 18 см, AA1 = DB.
- Гипотенуза АВ равнобедренного прямоугольного треугольника АВС равна 12 см. Точка N — середина катета АС. Найдите расстояние от точки N до прямой АВ.
- В треугольнике АВС известно, что АВ = 12 см, АС = 14 см. Через середину стороны ВС проведены прямые, параллельные сторонам АВ и АС. Найдите периметр образовавшегося четырёхугольника.
- Через точку М — середину боковой стороны CD трапеции ABCD — проведена прямая, параллельная стороне АВ и пересекающая основание AD в точке N. Найдите сторону АВ, если MN = 8 см.
- В окружности проведены хорды АВ и АС. Расстояние между точками В и С равно 16 см. Найдите расстояние от середины хорды АС до хорды А В, если ∠CBА = 30°.
- Диагональ трапеции делит её среднюю линию на отрезки, один из которых в 2 раза меньше другого. Найдите большее основание трапеции, если её меньшее основание равно 4 см.
- Большее основание трапеции равно 16 см. Диагонали трапеции пересекают её среднюю линию в точках Е и F. Найдите меньшее основание трапеции, если EF = 3 см.
- Боковую сторону трапеции разделили на 4 равных отрезка и через точки деления провели прямые, параллельные основаниям. Наименьший и наибольший отрезки этих прямых, принадлежащие трапеции, равны 9 см и 11 см. Найдите основания трапеции.
- Сторону ВС треугольника ABС разделили на 3 равных отрезка и через точки деления провели прямые, параллельные стороне AC. Найдите отрезки этих прямых, принадлежащие треугольнику ABС, если наибольший из этих отрезков на 5 см меньше стороны AC.
- В равнобедренном треугольнике ABС (AB = ВС) точка М пересечения медиан удалена от основания на 3 см. Найдите медиану треугольника ABС, проведённую к основанию.
- В прямоугольном треугольнике ABС (∠C = 90°) медианы пересекаются в точке М. Найдите отрезок СМ, если AB = 12 см.
- В равнобедренном треугольнике ABС (AB = ВС) точка пересечения медиан удалена от основания на 6 см. Найдите расстояние от середины боковой стороны треугольника ABС до основания.
- Отрезок AD — биссектриса треугольника ABС. Найдите:
1) отрезки BD и CD, если AB = 10 см, AC = 12 см, ВС = 11 см;
2) сторону AC, если BD : DC = 4 : 9, AB = 16 см;
3) стороны AB и AC, если AB + AC = 32 см, BD : DC = 5 : 3. - Стороны треугольника равны 12 см, 14 см и 16 см. Окружность, центр которой принадлежит средней по длине стороне треугольника, касается двух других сторон. Найдите отрезки, на которые центр окружности делит сторону треугольника.
- В треугольнике ABС AB = 8 см, ВС =11 см, AC = 5 см. В каком отношении центр окружности, вписанной в треугольник, делит его биссектрису С К?
- На медиане AD треугольника АВС отметили точку К так, что АК : KD = 7 : 6. В каком отношении прямая ВК делит сторону АС?
- На сторонах А В и ВС треугольника АВС отметили точки М и N соответственно. Отрезки AN и СМ пересекаются в точке О. В каком отношении точка О делит отрезок СМ, если AM : МВ = 5 : 3 и CN: NB = 9 : 16?
Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Теорема Фалеса. Теорема о пропорциональных отрезках». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!