Решебник задач по геометрии из учебного пособия Геометрия. 7-9 классы. УМК Атанасян и др. (Мнемозина).
Готовая домашняя работа
по учебнику: Геометрия 8 класс Атанасян
Глава V. Четырёхугольники
§ 1. Многоугольники (упр. 363 — 370).
§ 2. Параллелограмм и трапеция (упр. 371 — 398).
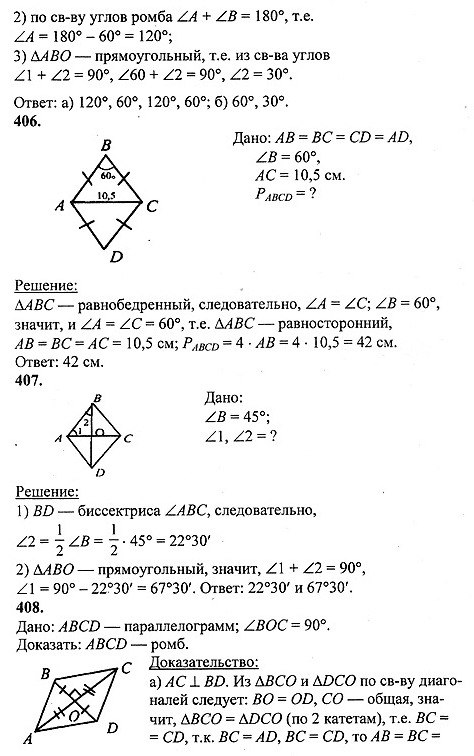
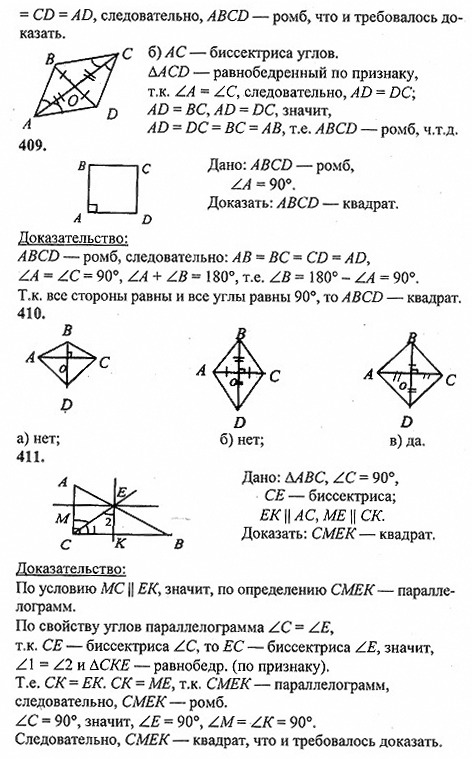
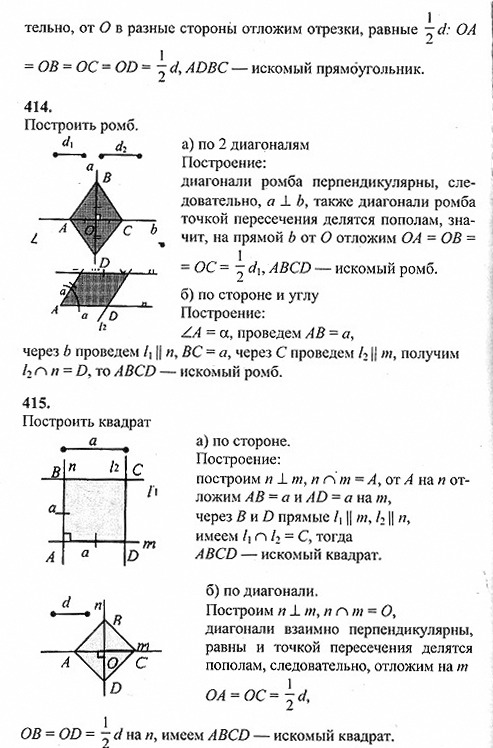
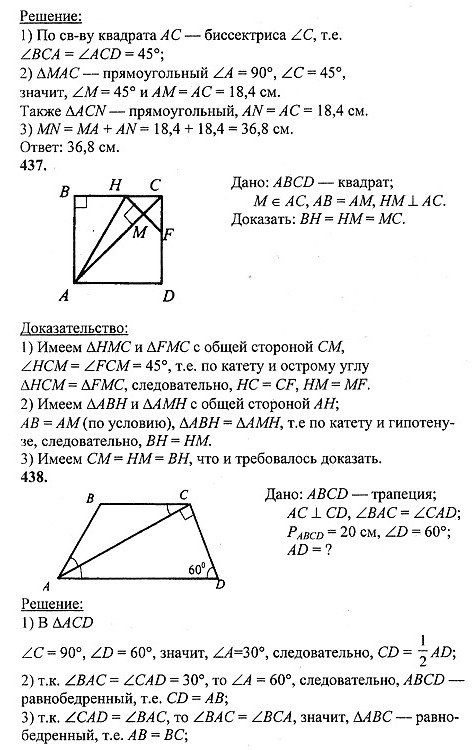
§ 3. Прямоугольник, ромб, квадрат (упр. 399 — 444).
Глава VI. Площадь
§ 1. Площадь многоугольника (упр. 445 — 458).
(материал готовится к публикации)
§ 2. Площади параллелограмма, треугольника и трапеции (упр. 459 — 482).
(материал готовится к публикации)
§ 3. Теорема Пифагора (упр. 483 — 532).
(материал готовится к публикации)
Глава VII Подобные треугольники
§ 1. Определение подобных треугольников (упр. 533 — ).
§ 2. Признаки подобия треугольников ().
§ 3. Применение подобия к доказательству теорем и решению задач ().
§ 4. Соотношения между сторонами и углами прямоугольного треугольника ().
Глава VIII Окружность
§ 1. Касательная к окружности ().
§ 2. Центральные и вписанные углы ().
§ 3. Четыре замечательные точки треугольника ().
§ 4. Вписанная и описанная окружности ().
Глава IX Векторы.
§ 1. Понятие вектора ().
§ 2. Сложение и вычитание векторов ().
§ 3. Умножение вектора на число. Применение векторов к решению задач ().
Решебник задач по геометрии из учебного пособия Геометрия. 7-9 классы. УМК Атанасян и др. (Мнемозина).