Конспект по физике для 8 класса «Скорость при неравномерном движении». Что такое мгновенная скорость. Как по графику скорости определить пройденный телом путь.
Конспекты по физике Учебник физики Тесты по физике
Скорость при неравномерном движении
В окружающем нас мире равномерное движение встречается нечасто. Обычно скорость тела изменяется с течением времени.
СРЕДНЯЯ СКОРОСТЬ НЕРАВНОМЕРНОГО ДВИЖЕНИЯ
В качестве примера неравномерного движения рассмотрим движение автобуса по шоссе. Начиная движение после остановки, автобус увеличивает свою скорость и, двигаясь далее, уменьшает свою скорость перед следующей остановкой. Он также может изменять скорость при пересечении перекрёстков, у светофора и т. п.
Необходимо чётко понимать, что когда мы говорим о скорости неравномерного движения, то имеем в виду скорость тела именно в данный момент времени. Однако если мы хотим охарактеризовать неравномерное движение в целом за данный промежуток времени, то вводится понятие средней скорости.
Средней скоростью неравномерного движения называют физическую величину, равную отношению пути, пройденного телом, ко времени, за которое этот путь был пройден:
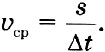
При таком способе описания движения мы фактически заменяем неравномерное движение равномерным, скорость которого равна средней скорости неравномерного движения.
Так как средняя скорость равна отношению двух скалярных величин, она сама является величиной скалярной. Зная среднюю скорость неравномерного движения, можно делать выводы о том, насколько быстро или медленно движется тело.
МГНОВЕННАЯ СКОРОСТЬ
При движении тело проходит последовательно все точки траектории. В каждой точке оно находится в определённые моменты времени и имеет определённую скорость.
Скорость тела в данный момент времени или в данной точке траектории называют мгновенной скоростью.
Для уяснения смысла мгновенной скорости потребуются дополнительные рассуждения. Например, как определить мгновенную скорость автобуса в некоторый момент времени t, соответствующий началу торможения?
По мере уменьшения промежутков времени фактическое движение в пределах каждого отдельного промежутка времени будет всё меньше отличаться от равномерного, и наконец отличие перестанет улавливаться приборами.
В пределах малых промежутков времени, столь малых, что движение представляется равномерным, результат измерения можно относить к любому моменту времени в пределах рассматриваемого промежутка. Если движение равномерно, то его мгновенная скорость в любой момент времени равна скорости этого равномерного движения.
Для иллюстрации понятия мгновенной скорости Р. Фейнман использует пример с машиной, остановленной полицейским в момент превышения скорости. Если в данный момент времени мгновенная скорость равна, например, 90 км/ч, то это означает, что, если начиная с этого момента времени машина двигалась бы равномерно и прямолинейно, за следующую секунду она прошла бы 25 м, а в течение последующего часа — 90 км.
Интересно, что Галилей не пользовался такой физической величиной, как скорость. Рассуждения о природе движения проводились в виде анализа отношений однородных, имеющих одинаковую размерность величин. Впервые в современной форме записи скорость ввёл Л. Эйлер в 1765 г. в работе «Теория движения твёрдых тел». Он писал: «При равномерном движении отношение путей к промежуткам времени, в течение которых они проходятся, называется быстротой или скоростью…» Эйлер впервые записал υ = s/t, и эта форма записи с тех пор не изменилась.
ГРАФИК СКОРОСТИ И ЗНАЧЕНИЕ ПЕРЕМЕЩЕНИЯ
Мы уже знаем, что при равномерном движении модуль перемещения равен площади под графиком скорости. Оказывается, при неравномерном движении это равенство также справедливо. При этом не имеет значения, как изменяется скорость с течением времени.
Построим график зависимости скорости от времени и разобьём весь интервал движения на отрезки Δt. Рассмотрим движение тела в отдельном промежутке времени Δt. Как определить площадь фигуры под графиком? Очевидно, что эта площадь больше площади прямоугольника S1 и меньше площади прямоугольника S2 (SABEF = S1; SACDF = S2)
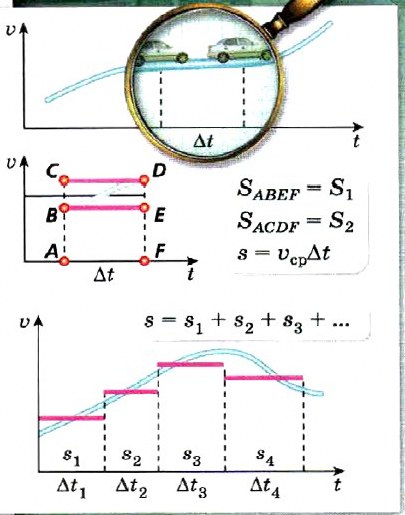
Если выбирать промежуток времени Δt всё меньше и меньше, то скорость на каждом промежутке времени будет меняться всё меньше и меньше и площади S1 и S2 будут отличаться всё меньше и меньше. Наконец, для каждого промежутка времени площадь под графиком станет равна произведению высоты (мгновенной скорости) и основания (промежутка времени), т. е. площадь равна перемещению тела за этот промежуток времени. А площадь под всем графиком равна сумме площадей для каждого промежутка времени, т. е. значение перемещения при неравномерном движении равно площади под графиком скорости.
Леонард Эйлер (1707—1783) — великий математик, механик и физик, швейцарец по происхождению. В 1727 г. переехал в Россию. Здесь работал в Петербургской академии наук.
Вы смотрели Конспект по физике для 8 класса «Скорость при неравномерном движении».
Вернуться к Списку конспектов по физике (Оглавление).