Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 26. Комбинаторные и вероятностные задачи к главе 3. ОТВЕТЫ на упражнения 26.1 — 26.7. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 26.1 — 26.7)
§ 26. Комбинаторные и вероятностные задачи к главе 3
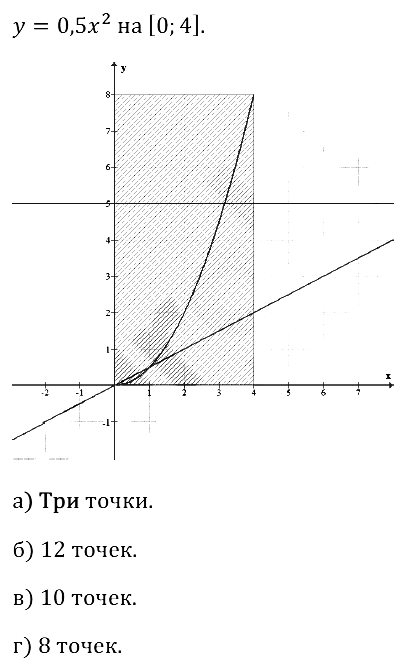
Задание № 26.1. Нарисуйте график функции у = 0,5х2 на отрезке [0; 4]. Сколько точек с целыми координатами:
а) принадлежит этому графику;
б) лежит ниже графика и выше оси абсцисс;
в) лежит выше графика и ниже прямой у = 5;
г) лежит ниже графика и выше прямой у = 0,5х ?
Задание № 26.2. Сколько точек, координаты которых – натуральные числа, лежит на графике функции:
а) у = 1/х; б) у = 5/х; в) у = 6/х; г) у = 12/х.
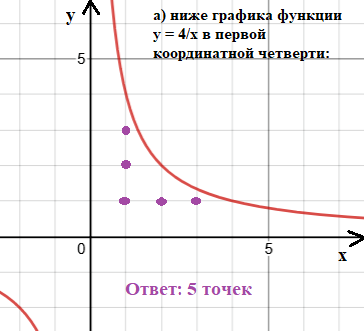
Задание № 26.3. Сколько точек с целочисленными координатами лежит:
а) ниже графика функции у = 4/х в первой координатной четверти*;
б) выше графика функции у = 5/х в третьей координатной четверти*;
в) ниже графика функции у = –3/x во второй координатной четверти*;
г) между графиками функций у = 2/x и у = –2/x (не включая точки на координатных осях)?
*- не на осях координат
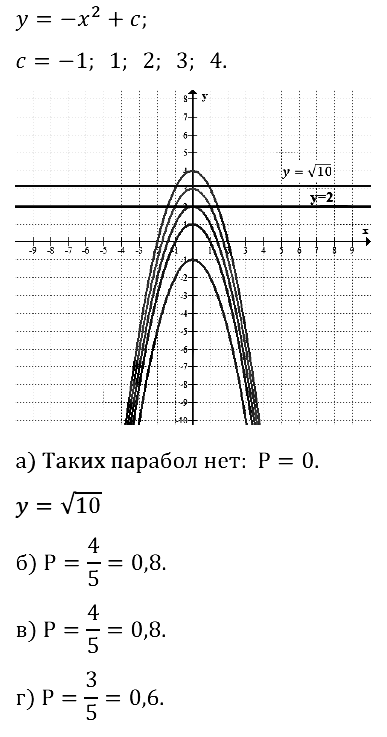
Задание № 26.4. В уравнении параболы у = –х2 + с коэффициент с случайным образом выбирают из чисел –1, 1, 2, 3, 4. Какова вероятность того, что эта парабола:
а) не пересечёт четвёртую координатную четверть;
б) будет расположена ниже прямой у = √10;
в) пересечёт ось абсцисс в двух точках;
г) будет иметь хотя бы одну общую точку с прямой у = 2?
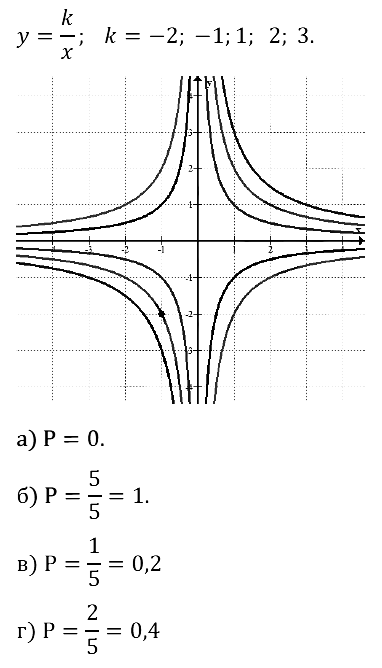
Задание № 26.5. Коэффициент k случайным образом выбирают из чисел –2, –1, 1, 2, 3. Какова вероятность того, что график функции у = k/x:
а) пересекает и первую, и вторую координатную четверть;
б) симметричен относительно начала координат;
в) проходит через точку (– 1, – 2);
г) содержит ровно две точки с целочисленными координатами?
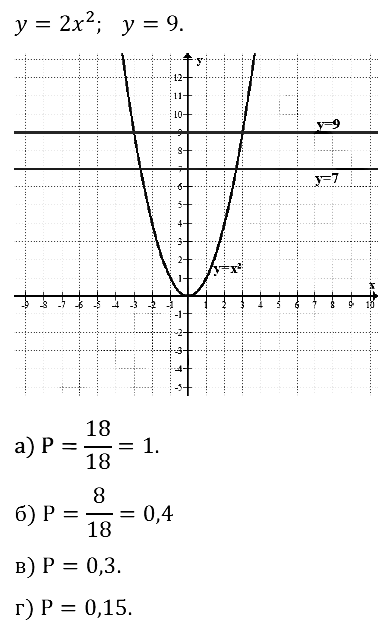
Задание № 26.6. Случайным образом выбирают точку с целочисленными координатами так, чтобы она лежала выше графика функции у = 2х2 и ниже графика прямой у = 9. Какова вероятность того, что эта точка лежит:
а) выше оси абсцисс; в) левее оси ординат;
б) на оси ординат; г) выше прямой у = 7?
Задание № 26.7. В прямоугольнике АСКМ (рис. 69) надо пройти по отмеченным линиям из вершины А в вершину К, двигаясь только вверх или вправо. Сколько всего путей: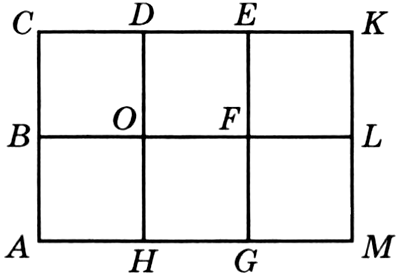
а) проходит через вершину М;
б) проходит через точку Н;
в) проходит через точку В;
г) можно проложить из вершины А в вершину К?
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 26. Комбинаторные и вероятностные задачи к главе 3. ОТВЕТЫ на упражнения 26.1 — 26.7. Вернуться в ОГЛАВЛЕНИЕ.