Упражнения: Прямоугольник

Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Прямоугольник». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.

Прямоугольник

Вариант 1

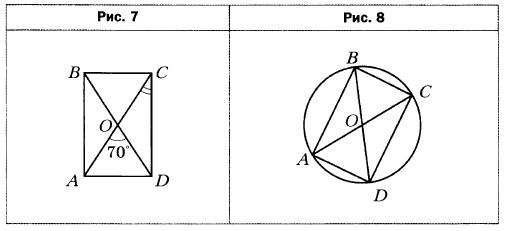
32. Диагонали прямоугольника АВCD (рис. 7) пересекаются в точке О, ∠AOD = 70°. Найдите угол OCD.
33. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол ABD, если он на 30° больше угла COD.
34. В окружности с центром О проведены диаметры АС и BD (рис. 8). Докажите, что четырёхугольник ABCD является прямоугольником. Найдите отрезок ВС, если АС= 18 см, ∠ABD = 30°.
35. Диагонали параллелограмма ABCD пересекаются в точке О. Биссектриса угла AOD пересекает сторону AD в её середине. Докажите, что ABCD — прямоугольник.
36. Расстояние от точки пересечения диагоналей прямоугольника до его большей стороны на 5 см меньше, чем расстояние до меньшей стороны. Найдите стороны прямоугольника, если его периметр равен 44 см.
37. Сумма расстояний от точки пересечения диагоналей прямоугольника до его двух соседних сторон равна 27 см. Найдите стороны прямоугольника, если они относятся как 4:5.
38. Медиана прямоугольного треугольника, проведённая к гипотенузе, на 6 см меньше гипотенузы. Найдите медиану, проведённую к гипотенузе.
39. В треугольнике АВС известно, что АВ = 10 см, ∠А = 20°, ∠В = 70°. Найдите медиану треугольника, проведённую к стороне АВ.
40. В окружности проведены перпендикулярные хорды АВ и ВС. Длина отрезка, соединяющего середины этих хорд, равна 8 см. Найдите расстояние от центра окружности до точки В.

Вариант 2

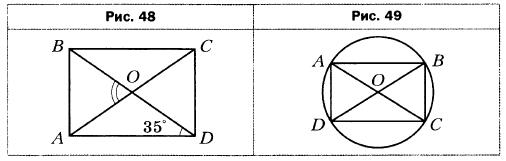
32. Диагонали прямоугольника ABCD (рис. 48) пересекаются в точке О, ∠ODA = 35°. Найдите угол АОВ.
33. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол COD, если он в 4 раза меньше угла ABD.
34. В окружности с центром О проведены диаметры АС и BD (рис. 49). Докажите, что четырёхугольник ABCD является прямоугольником. Найдите отрезок BD, если AD = 7 см, ∠ACD = 30°.
35. Диагонали параллелограмма ABCD пересекаются в точке О. Медиана ОМ треугольника ВОС перпендикулярна стороне ВС. Докажите, что ABCD — прямоугольник.
36. Расстояние от точки пересечения диагоналей прямоугольника до его большей стороны на 6 см меньше, чем расстояние до меньшей стороны. Найдите стороны прямоугольника, если его периметр равен 48 см.
37. Сумма расстояний от точки пересечения диагоналей прямоугольника до его двух соседних сторон равна 24 см. Найдите стороны прямоугольника, если они относятся как 7:9.
38. Разность гипотенузы прямоугольного треугольника и проведённой к ней медианы равна 7 см. Найдите гипотенузу.
39. В треугольнике АВС известно, что ∠A = 75°, ∠B = 15°. Медиана, проведённая к стороне АВ, равна 2 см. Найдите сторону АВ.
40. В окружности проведены перпендикулярные хорды MN и МК. Расстояние от центра окружности до точки М равно 10 см. Найдите длину отрезка, соединяющего середины хорд.

Вариант 3

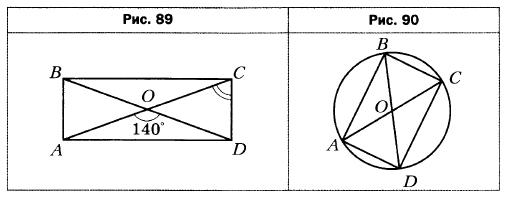
32. Диагонали прямоугольника ABCD (рис. 89) пересекаются в точке О, ∠AOD = 140°. Найдите угол OCD.
33. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол ADB, если он на 135° меньше угла ВОС.
34. В окружности с центром О проведены диаметры АС и BD (рис. 90). Докажите, что четырёхугольник ABCD является прямоугольником. Найдите угол ABD, если АС = 12 см, ВС = 6 см.
35. Диагонали параллелограмма ABCD пересекаются в точке О. Биссектриса угла COD перпендикулярна стороне CD. Докажите, что ABCD — прямоугольник.
36. Расстояние от точки пересечения диагоналей прямоугольника до его меньшей стороны на 8 см больше, чем расстояние до большей стороны. Найдите стороны прямоугольника, если его периметр равен 72 см.
37. Сумма расстояний от точки пересечения диагоналей прямоугольника до его двух соседних сторон равна 32 см. Найдите стороны прямоугольника, если они относятся как 3:5.
38. Сумма гипотенузы прямоугольного треугольника и проведённой к ней медианы равна 27 см. Найдите гипотенузу.
39. В треугольнике АВС известно, что АВ = 14 см, ∠A = 35°, ∠B = 55°. Найдите медиану треугольника, проведённую к стороне АВ.
40. В окружности проведены перпендикулярные хорды DE и DF. Длина отрезка, соединяющего середины этих хорд, равна 6 см. Найдите расстояние от центра окружности до точки D.

Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Прямоугольник». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки! 

Вернуться к Списку упражнений по геометрии УМК Мерзляк