Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2023). Глава I Алгебраические дроби. § 1. Основные понятия. ОТВЕТЫ на упражнения 1.1 — 1.41. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 1.1 — 1.41)
§ 1. Основные понятия
Является ли алгебраической дробью выражение:
№ 1.1. а) 3a2/5b2; б) (10x2 + 4x – 7)/8; в) c2/b2; г) 3/(9m – 5) ?
№ 1.2. а) (7a2 + 4)/14; б) (2f2 + 6f + 15)/2f – 5f; в) 3t – p2/t2; г) (6nm + 3m2n2)/(7n – 12m).
Найдите значение алгебраической дроби:
№ 1.3. а) (x – 2)/x при x = 3; б) (t – 7)2/2s при t = 4, s = –1; в) (y + 6)/(y – 2) при y = 4; г) (x – 5)/(2y + 3)2 при x = 2, y = –2.
№ 1.4. а) (p + 8)2/(p2 + 4) при p = –2; б) …
Установите, при каких значениях переменной не имеет смысла алгебраическая дробь:
№ 1.5. а) (а – 5)/(а + 5); б) 5с/(4 + 10с); в) …
№ 1.6. a) 9х2/(x(x + 2)); б) …
№ 1.7. a) (3а2 + 5) / ((а + 2)(а + 3)); б) …
№ 1.8. Найдите допустимые значения переменной для заданной алгебраической дроби:

№ 1.9. Придумайте примеры алгебраических дробей, которые имели бы смысл при: а) х ≠ 3; б) у ≠ 0, у ≠ 12; в) z ≠ –4, z ≠ –7, z ≠ 0; г) любом значении х.
Найдите значения переменной, при которых алгебраическая дробь равна нулю (если такие значения существуют):
№ 1.10.

№ 1.11.

№ 1.12. Зная, что a – 2b = 3, найдите значение выражения: а) 2b – а; б) 2а – 4b; в) (4b – 2a)/3; г) 6/(2a – 4b). Составьте математическую модель ситуации, описанной в условии задачи:
№ 1.13. Туристы прошли 6 км по лесной тропе, а затем 10 км по шоссе, увеличив при этом свою скорость на 1 км/ч. На весь путь они затратили 3,5 ч.
№ 1.14. Прогулочный катер двигался по реке, скорость течения которой 2 км/ч. По течению реки он проплыл 18 км, а против течения 14 км, затратив на весь путь 1 ч 20 мин.
№ 1.15. Из пункта А в пункт В, находящийся на расстоянии 120 км от пункта А, выехали одновременно два автомобиля. Скорость одного из них на 20 км/ч больше скорости другого, поэтому он приехал в пункт В на 1 ч раньше.
№ 1.16. Из города в посёлок, находящийся на расстоянии 40 км от города, выехал грузовик, а через 10 мин вслед за ним отправился легковой автомобиль, скорость которого на 20 км/ч больше скорости грузовика. В посёлок они прибыли одновременно.
№ 1.17. С двух турбаз одновременно вышли две группы туристов, которые должны были встретиться на берегу реки. До этого места первой группе нужно идти 12 км, а второй – 10 км. Известно, что скорость первой группы была на 1 км/ч меньше скорости второй и что она прибыла на берег реки на 1 ч позже второй группы.
Решите задачу, выделяя три этапа математического моделирования:
№ 1.18. Моторная лодка, собственная скорость которой равна 30 км/ч, прошла по течению реки расстояние 48 км и против течения 42 км. Какова скорость течения реки, если известно, что на путь по течению лодка затратила столько же времени, сколько на путь против течения?
№ 1.19. Автобус проходит расстояние 160 км за время, которое автомобиль тратит на прохождение 280 км. Найдите скорость автобуса, если известно, что она на 30 км/ч меньше скорости автомобиля.
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ЗГлава I Алгебраические дроби. § 1. Основные понятия. ОТВЕТЫ на упражнения 1.1 — 1.41. Вернуться в ОГЛАВЛЕНИЕ.


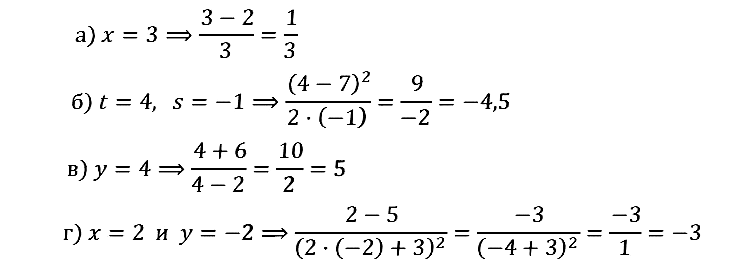
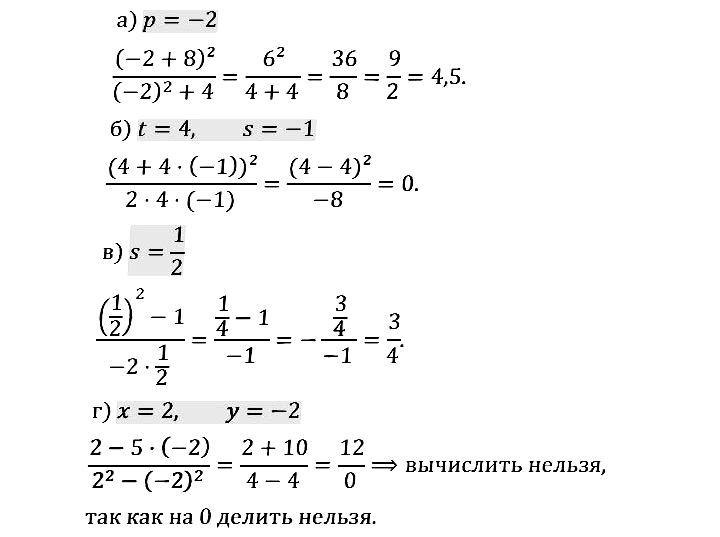
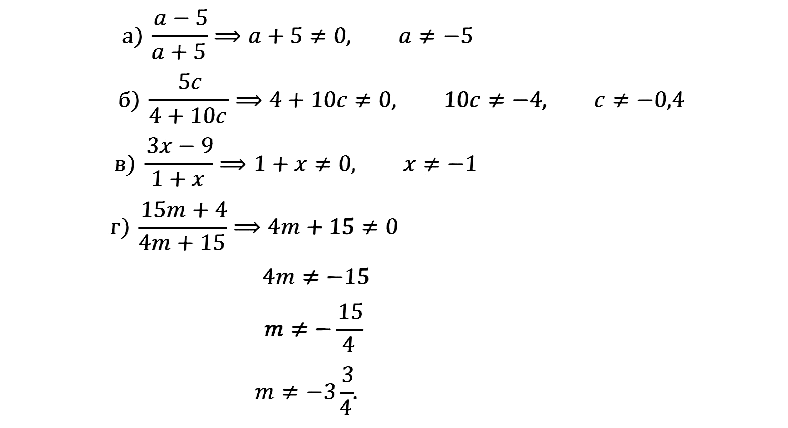
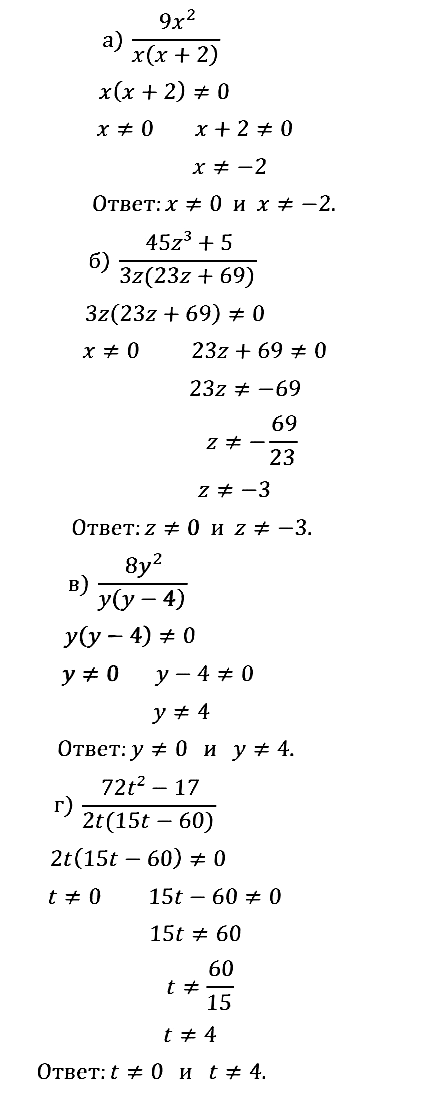
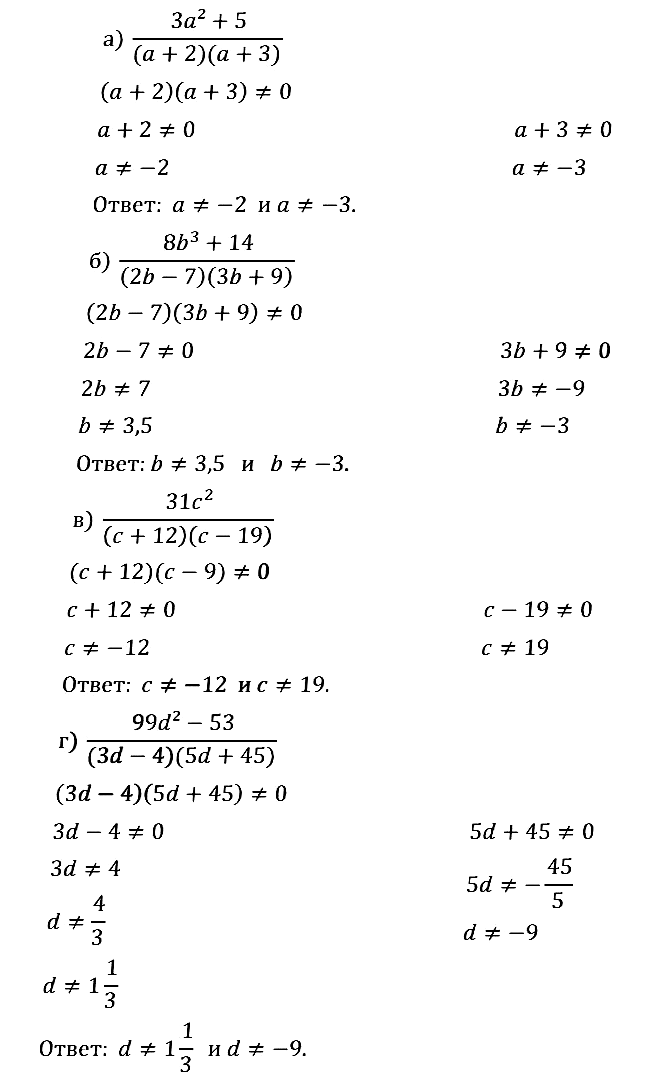
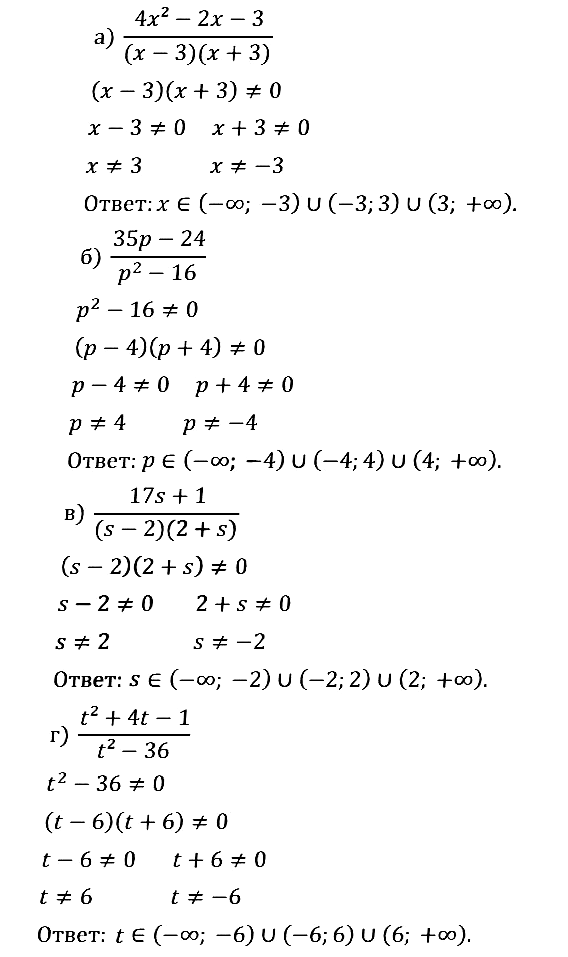
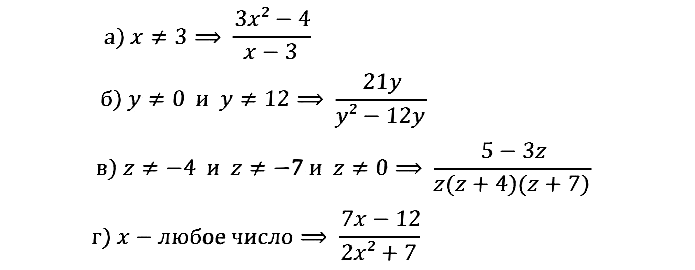


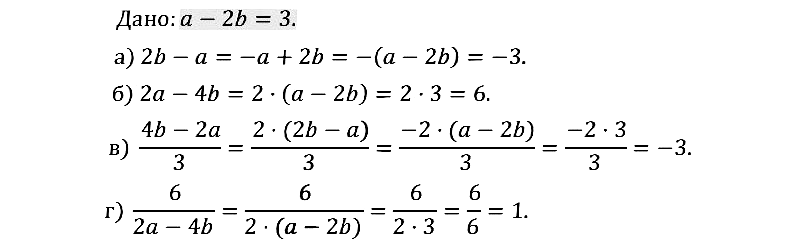







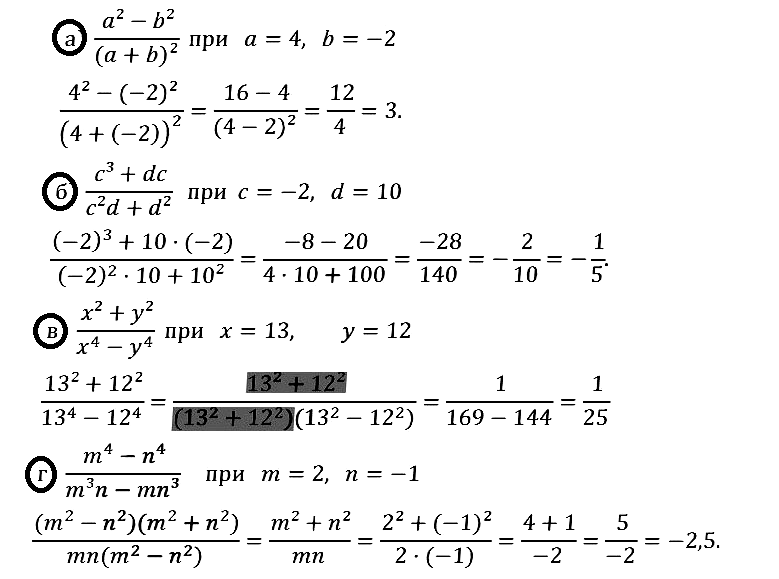






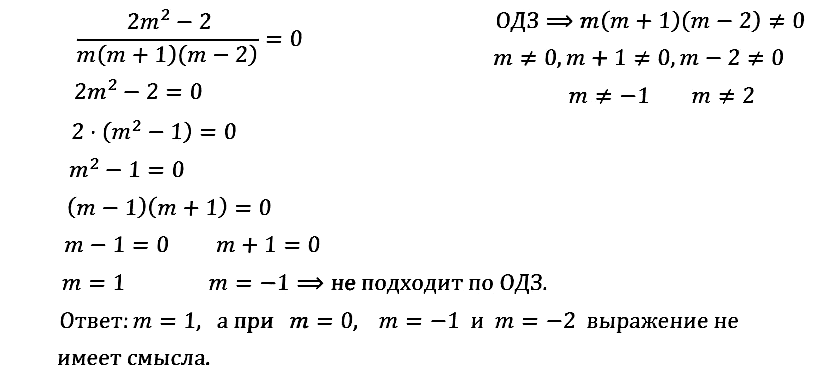


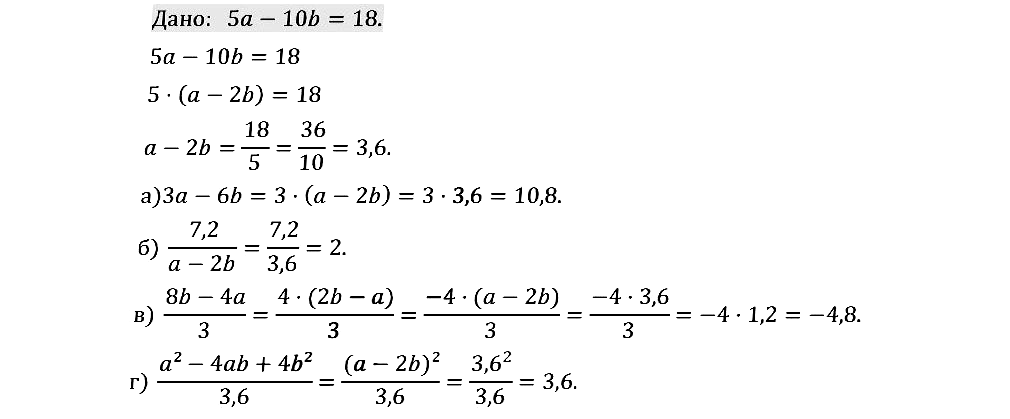
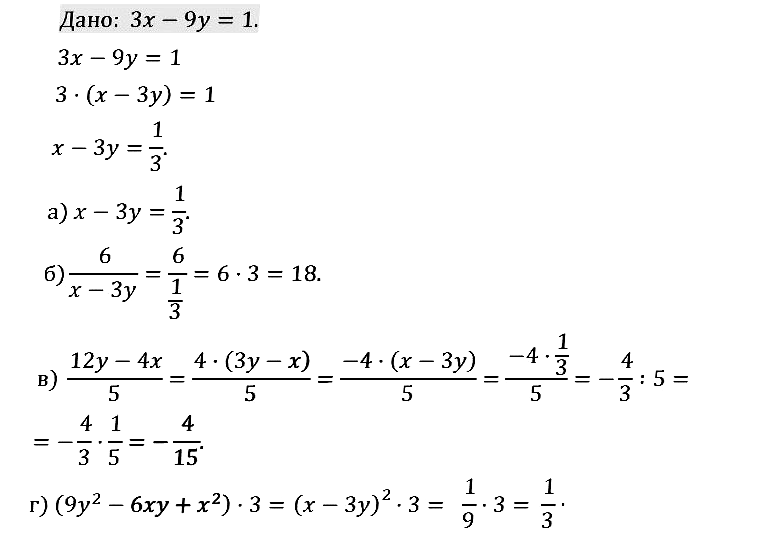
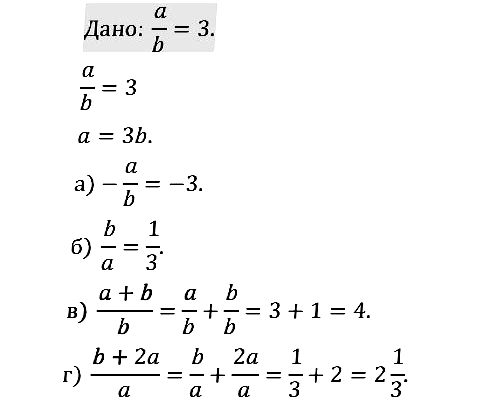
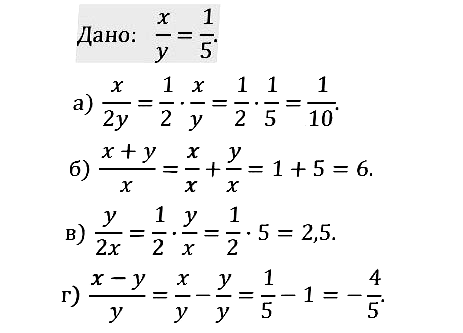
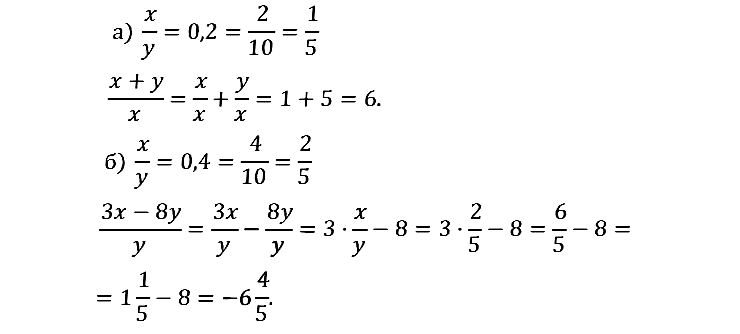
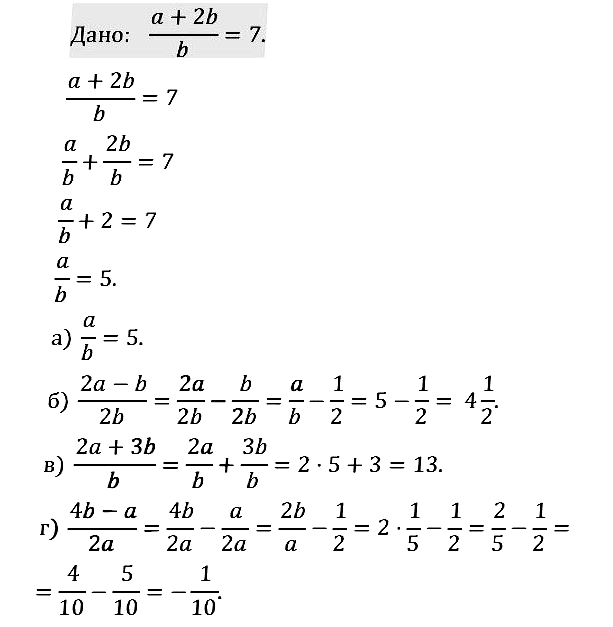
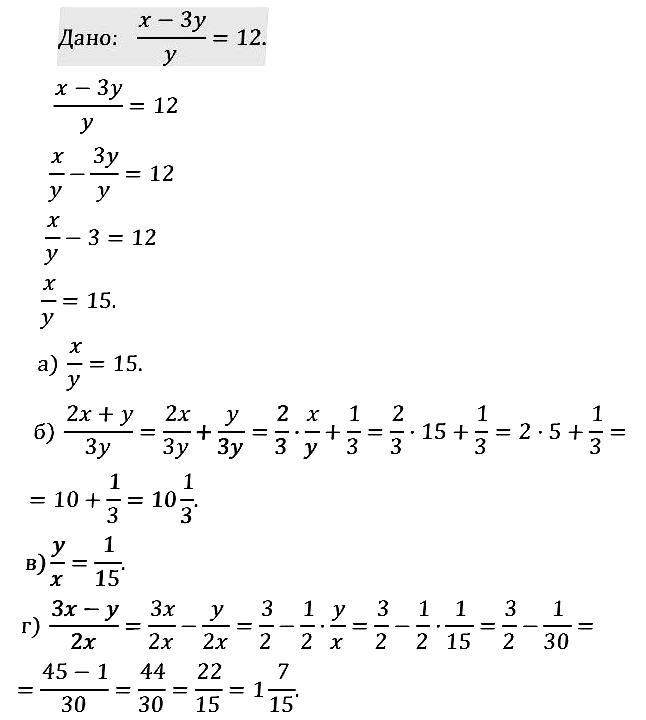

В номере 1.8 везде в ответах х принадлежит, а на деле во втором принадлежит р, в третьем s, в четвёртом еще что-то. А так отличный сайт, буду пользоваться!
Исправлено.
Номер 1.34 под г потерян квадрат при замене скобки по формуле квадрата разницы, И ответ будет 1:3
Исправлено.