Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). Задачи на повторение пройденного в 7 классе. ОТВЕТЫ на упражнения 35 — 68. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 35 — 68)
Задачи на повторение
№ 36. Изобразите на координатной прямой числовой промежуток, назовите его и запишите его аналитическую модель, используя знаки неравенств. Найдите наименьшее целое число, принадлежащее заданному промежутку: а) (2; +∞); б) (–∞; 6]; в) [1; 5]; г) [4; 10).
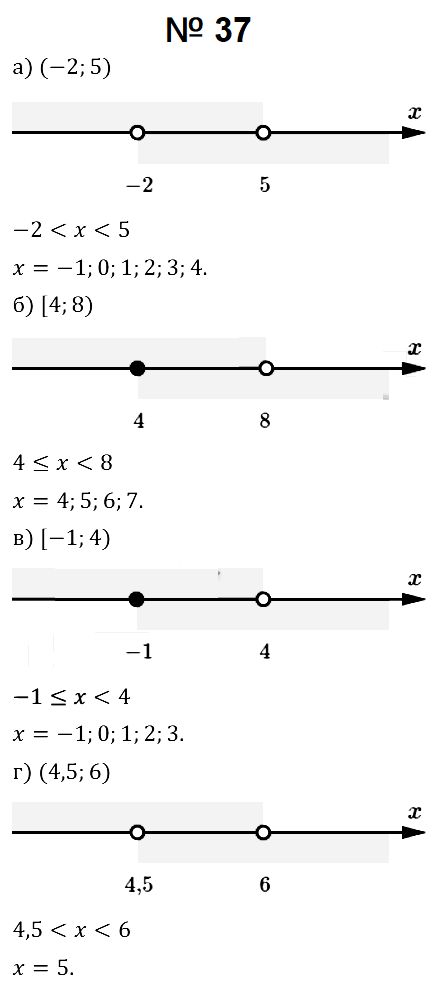
№ 37. Изобразите на координатной прямой числовой промежуток, назовите его и запишите его аналитическую модель, используя знаки неравенств. Укажите все целые числа, принадлежащие заданному промежутку: а) (–2; 5); б) [4; 8); в) [–1; 4); г) (4,5; 6).
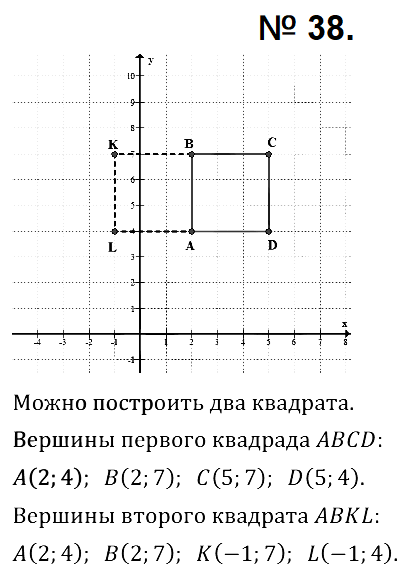
№ 38. На координатной плоскости отметьте точки А (2; 4) и В (2; 7). Изобразите квадрат, одной из сторон которого служит отрезок АВ. Найдите координаты вершин квадрата. Сколько таких квадратов можно построить?
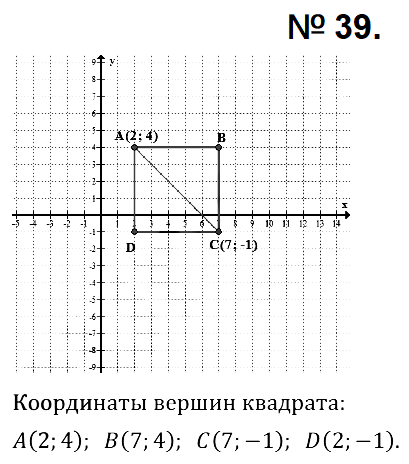
№ 39. На координатной плоскости отметьте точки А (2; 4) и С (7; –1). Изобразите квадрат, диагональю которого служит отрезок АС. Найдите координаты вершин квадрата.
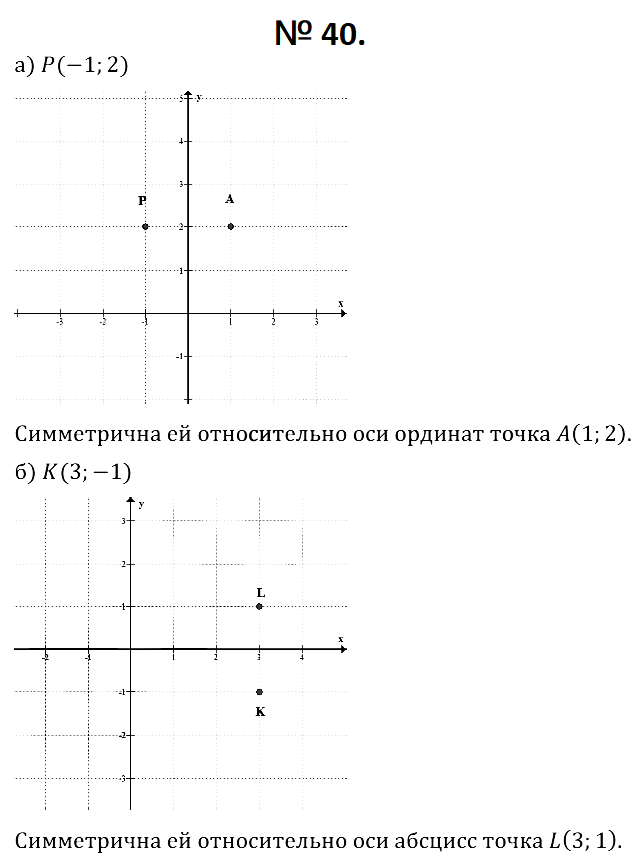
№ 40. а) Отметьте на координатной плоскости точку Р (–1; 2). Найдите точку, симметричную данной относительно оси ординат.
б) Отметьте на координатной плоскости точку К (3; –1). Найдите точку, симметричную данной относительно оси абсцисс.
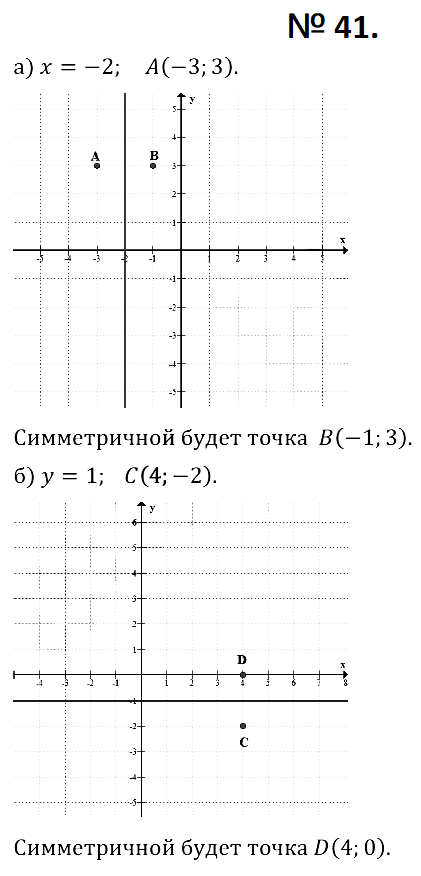
№ 41. а) Изобразите на координатной плоскости точку А (–3; 3) и прямую х = –2. Найдите точку, симметричную данной относительно построенной прямой.
б) Изобразите на координатной плоскости точку С (4; –2) и прямую у = 1. Найдите точку, симметричную данной относительно построенной прямой.
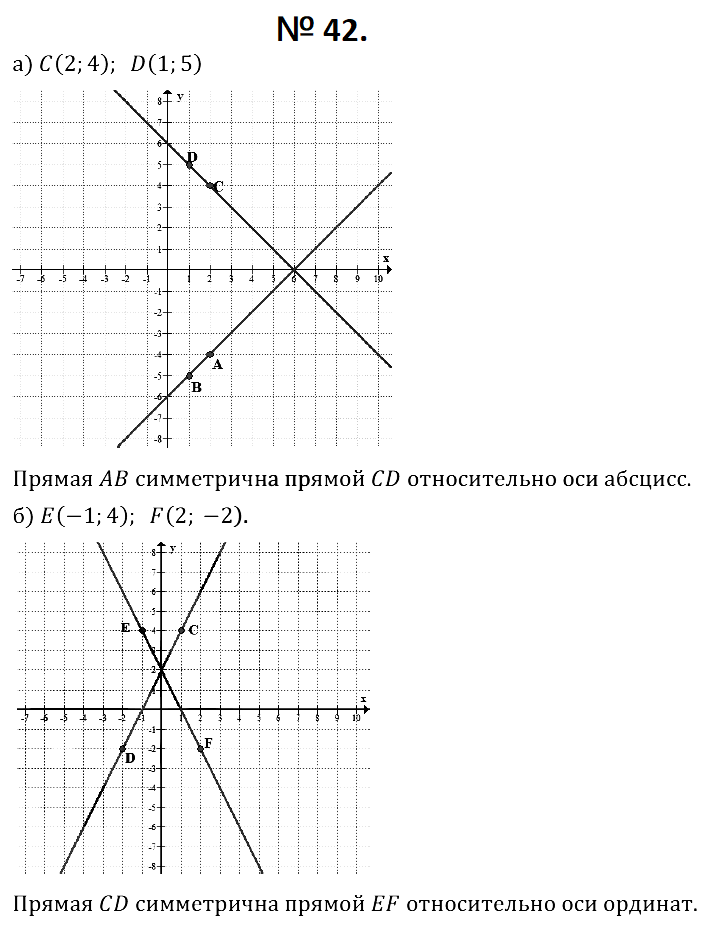
№ 42. а) Даны точки С (2; 4) и D (1; 5). Постройте прямую, симметричную прямой CD относительно оси абсцисс.
б) Даны точки E (–1; 4) и F (2; –2). Постройте прямую, симметричную прямой EF относительно оси ординат.
№ 43. Постройте график функции у = х – 5. Определите:
а) при каком значении аргумента выполняется равенство у = –3;
б) чему равно значение функции в точке х = –3;
в) при каких значениях аргумента функция принимает положительные значения;
г) при каких значениях аргумента функция принимает значения, меньшие чем 3;
д) возрастает или убывает функция.
№ 44. Постройте график функции у = –х + 4. Определите:
а) при каком значении аргумента выполняется равенство у = 0;
б) чему равно значение функции в точке х = –1;
в) при каких значениях аргумента функция принимает отрицательные значения;
г) при каких значениях аргумента функция принимает значения, меньшие чем 5;
д) возрастает или убывает функция.
№ 45. Постройте график функции у = 2х + 3. Определите:
а) при каком значении аргумента выполняется равенство у = 7;
б) чему равно значение функции в точке х – –2;
в) при каких значениях аргумента функция принимает отрицательные значения;
г) при каких значениях аргумента функция принимает значения, большие чем 3;
д) возрастает или убывает функция.
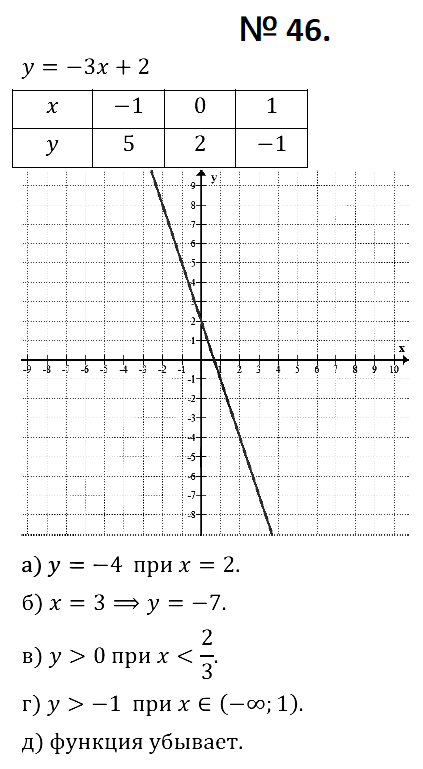
№ 46. Постройте график функции у = –3х + 2. Определите:
а) при каком значении аргумента выполняется равенство у = – 4;
б) чему равно значение функции в точке х = 3;
в) при каких значениях аргумента функция принимает положительные значения;
г) при каких значениях аргумента функция принимает значения, большие чем –1;
д) возрастает или убывает функция.
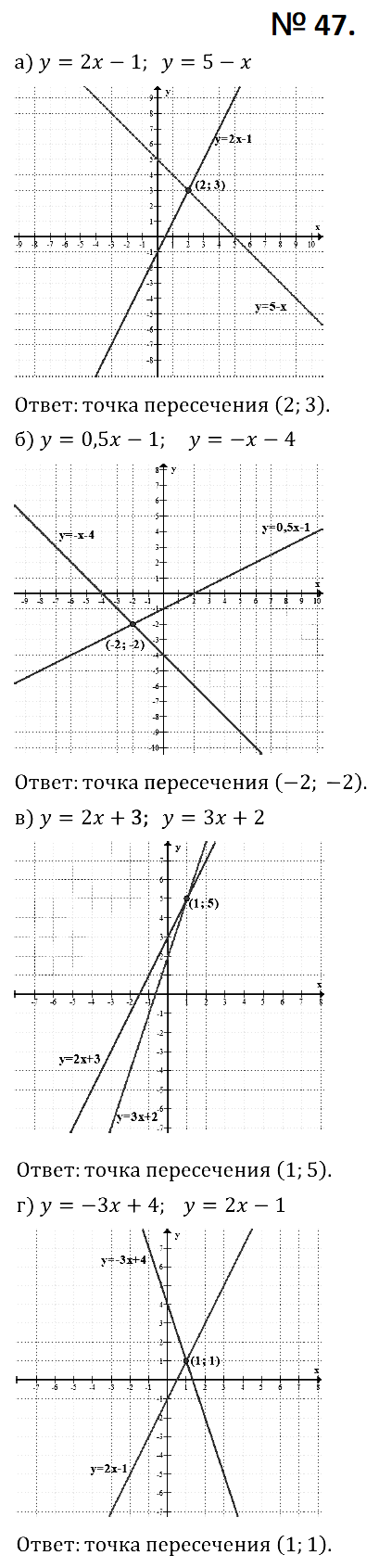
№ 47. Найдите точку пересечения графиков функций:
а) у = 2х – 1 и у = 5 – х; в) у = 2х + 3 и у = 3х + 2;
б) y = 0,5x – 1 и у = –х – 4; г) у = –3х + 4 и y = 2х – 1.
№ 48. Постройте график функции y = х2. Найдите:
а) значения функции при значении аргумента, равном –3; 1; 2;
б) значения аргумента, если значение функции равно 0; 1; 9;
в) наибольшее и наименьшее значения функции на отрезке [–2; 0];
г) координаты точки пересечения параболы и прямой у = 4.
№ 49. Постройте график функции у = –х2. Найдите:
а) значения функции при значении аргумента, равном –3; –2; 1;
б) значения аргумента, если значение функции равно 0; –1; – 4;
в) наименьшее и наибольшее значения функции на отрезке [–1; 3];
г) координаты точек пересечения параболы у = –х2 и прямой y = 2х.
№ 50. Решите графически уравнение: а) х2 = х + 2; б) х2 = –х + 6; в) х2 = 2х + 3; г) х2 = –3х.
№ 51. Функция задана формулой у = f(х), где f(x) = 2х – 6.
а) Найдите: f(–1), f(0), f(3). б) Решите уравнение f(2х) = 4.
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). Задачи на повторение пройденного в 7 классе. ОТВЕТЫ на упражнения 35 — 68. Вернуться в ОГЛАВЛЕНИЕ.
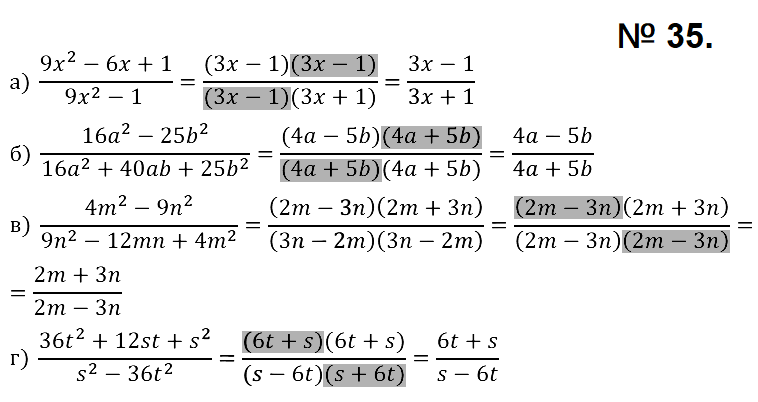
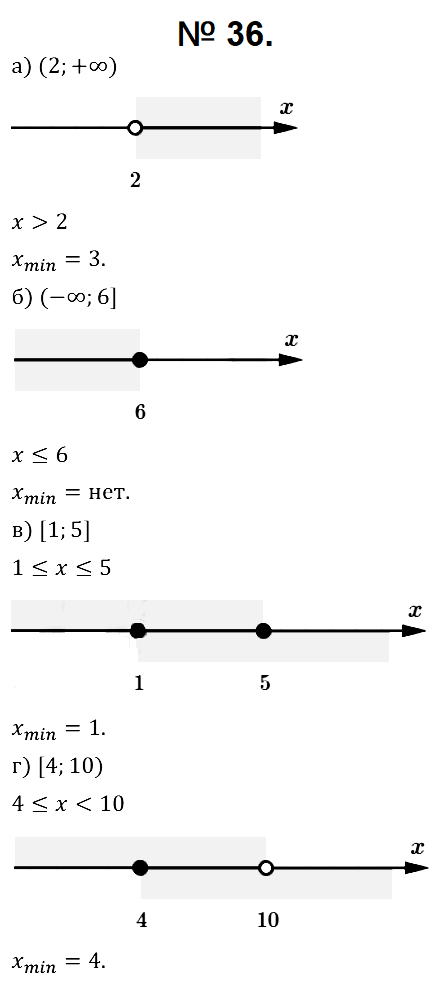
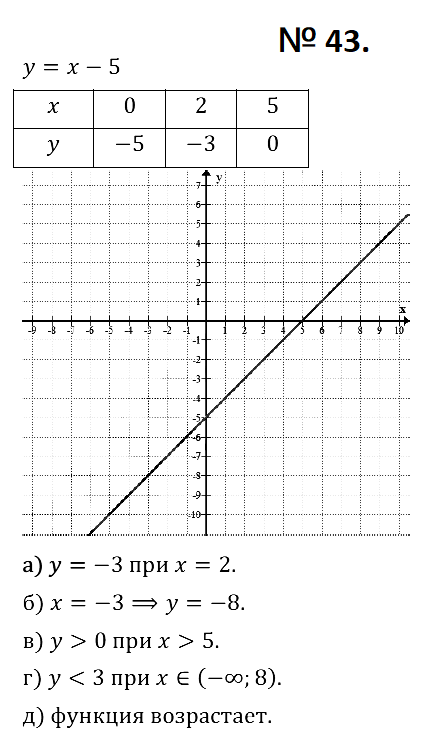
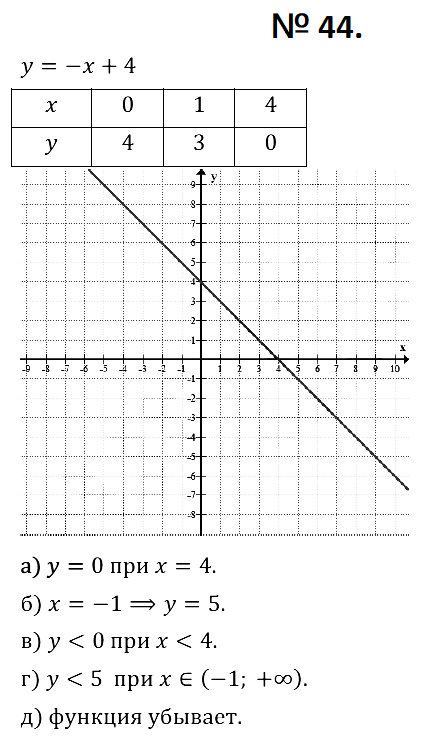
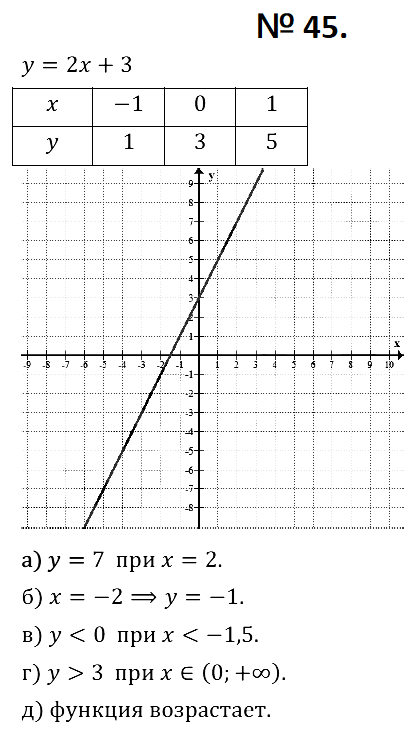
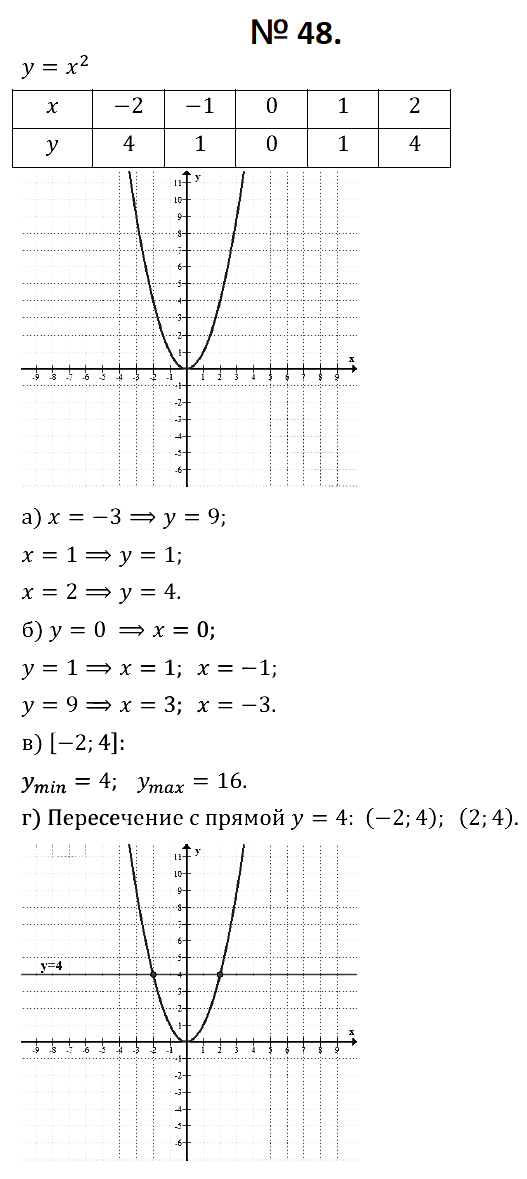
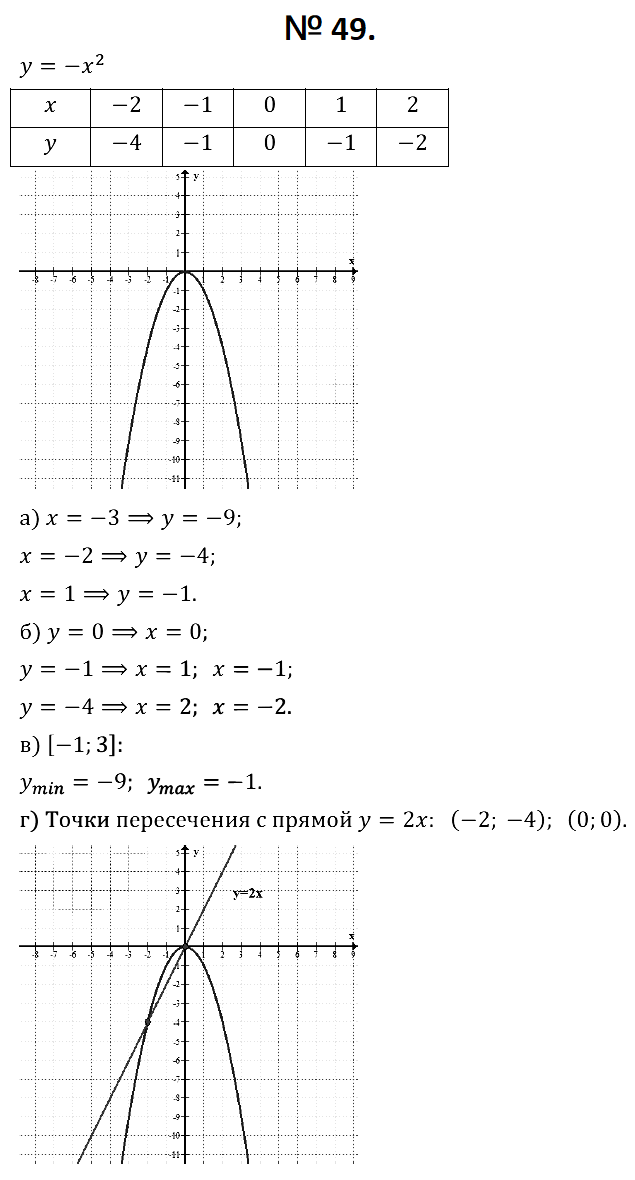
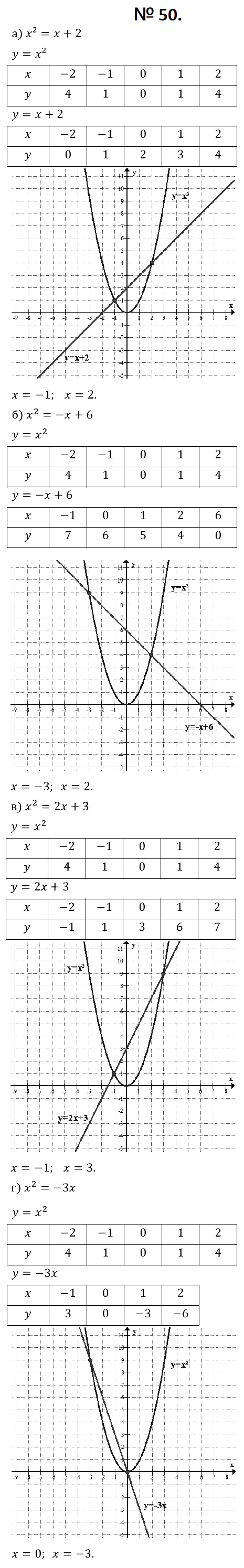
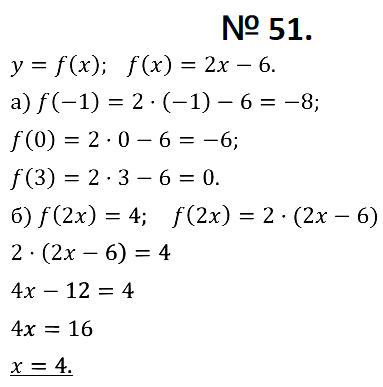
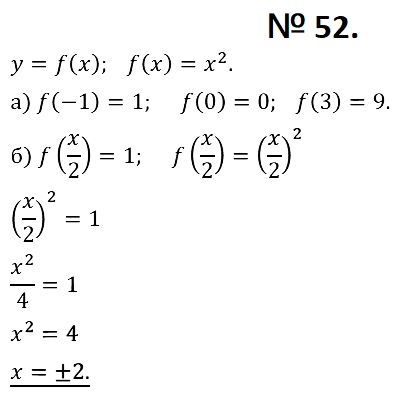

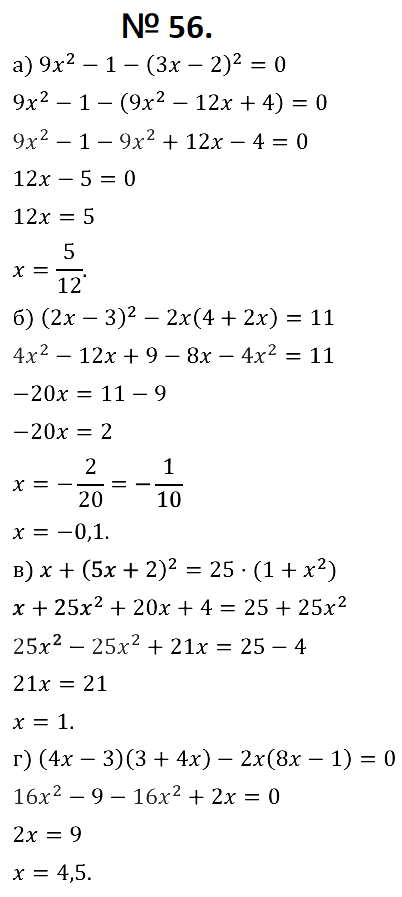

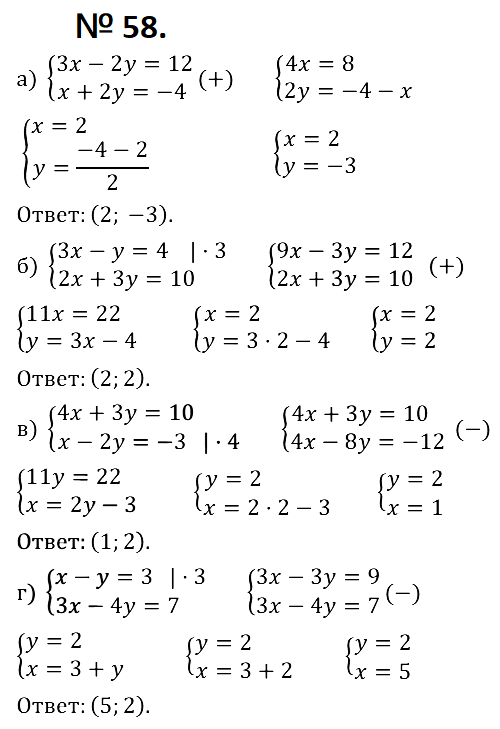
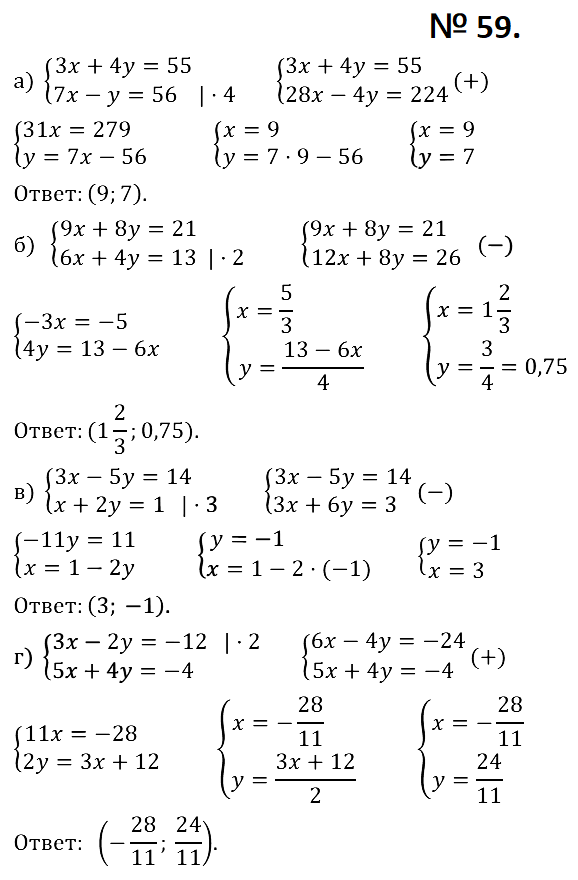









ответ в 41 б неверный: там не y=-1, а y=1 => B(4;4).