Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 18. Комбинаторные и вероятностные задачи. Правило умножения. ОТВЕТЫ на упражнения 18.1 — 18.7. ГЛАВА 2. ФУНКЦИЯ у = √x. СВОЙСТВА КВАДРАТНОГО КОРНЯ. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 18.1 — 18.7)
§ 18. Комбинаторные и вероятностные задачи. Правило умножения
Задание № 18.1. В записи * ∉ ■ вместо * можно поставить одно из чисел: -3, 0,(317), 17/3, √3, а вместо ■ — один из символов числовых множеств: N, Z, Q. Будут получаться различные утверждения (верные или неверные), например: –3 ∈ N, √3 ∉ Q и т.п.
а) Сколько получится утверждений, у которых на последнем месте стоит Z?
б) Изобразите дерево вариантов составления всевозможных утверждений.
в) Сколько всего утверждений получится?
г) Сколько среди них верных утверждений?
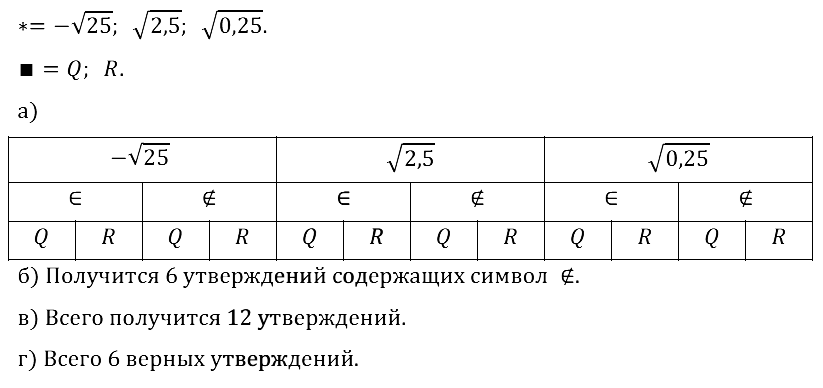
Задание № 18.2. В записи * Ω ■ вместо * можно произвольно поставить одно из чисел: –√25, √2,5, √0,25, вместо Ω — поставить ∈ или ∉, а вместо ■ – символ числового множества Q или R.
а) Изобразите дерево вариантов составления таких утверждений.
б) Сколько получится утверждении, содержащих символ ∉ ?
в) Сколько всего утверждений получится?
г) Сколько среди них верных утверждений?
Задание № 18.3. а) Между любыми цифрами числа 123 456 789 можно поставить запятую. Сколько при этом получится десятичных дробей?
Какова вероятность того, что после вставки запятой получится число:
б) больше миллиона; в) меньше ста; г) дробная часть которого больше 0,3?
Задание № 18.4. Дано выражение √[n + 1]. Значение переменной n случайно выбирают среди целых чисел от 0 до 99 включительно.
а) Сколько всего значений может принять данное выражение?
б) Сколько среди них целых чисел?
в) Сколько среди них иррациональных чисел?
r) Сколько среди них чисел больше семи?
Задание № 18.5. Рассматриваются отличные от нуля целые числа, модуль которых меньше 11.
а) Сколько всего существует таких чисел?
б) Сколько среди них отрицательных чисел?
в) Сколько среди них чисел, модуль которых больше 7?
г) Сколько среди них чисел из промежутка (–10; –1)?
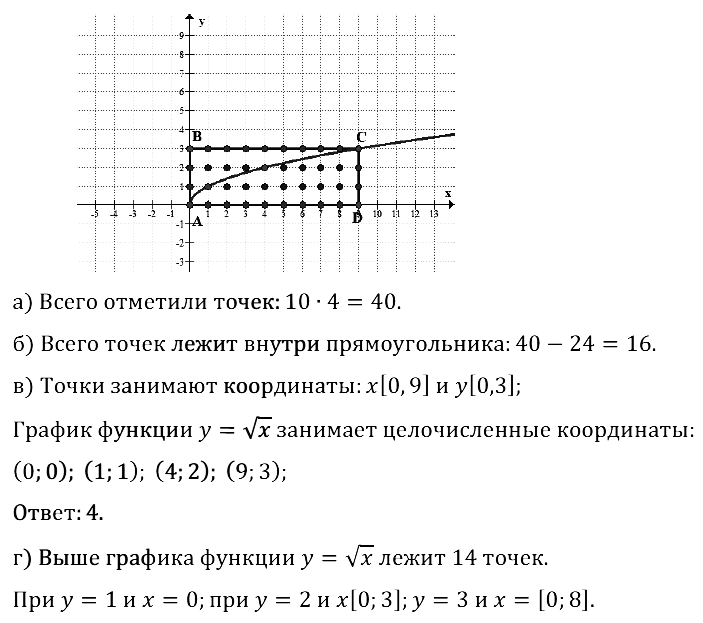
Задание № 18.6. В прямоугольнике с вершинами А(0; 0), В(0; 3), С(9; 3), D(9; 0) отметили все точки с целочисленными координатами.
а) Сколько всего отметили точек (включая точки, лежащие на сторонах)?
б) Сколько таких точек лежит внутри (не на сторонах) прямоугольника?
в) Сколько таких точек лежит на графике функции у = √х ?
г) Сколько таких точек лежит выше графика функции у = √x ?
Задание № 18.7. В квадрате ACEG надо пройти по отмеченным линиям (рис. 8) из вершины А в вершину Е, двигаясь только вверх или вправо.
а) Выпишите все пути, проходящие через вершину G.
б) Сколько путей проходит через точку Н?
в) Сколько путей проходит через точку В?
г) Сколько всего имеется таких путей?
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 2. ФУНКЦИЯ у = √x. СВОЙСТВА КВАДРАТНОГО КОРНЯ. § 18. Комбинаторные и вероятностные задачи. Правило умножения. ОТВЕТЫ на упражнения 18.1 — 18.7. Вернуться в ОГЛАВЛЕНИЕ.