Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). § 32. Теорема Виета и её применения. ОТВЕТЫ на упражнения 32.1 — 31.55. ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 32.1 — 32.55)
§ 32. Теорема Виета и её применения
Задание № 32.1. У какого из заданных квадратных уравнений сумма корней равна –6, а произведение корней равно –11:
а) x2 – 6х + 11 = 0; б) x2 + 6x – 11 = 0; в) x2 – 11х – 6 = 0; г) x2 + 11x – 6 = 0 ?
Не решая уравнения, определите, имеет ли оно корни. Для уравнений, имеющих корни, найдите их сумму и произведение:
Задание № 32.2. а) x2 + 2х – 5 = 0; б) x2 – 15x + 16 = 0; в) x2 – 19x + 1 = 0; г) x2 + 8x + 10 = 0.
Задание № 32.3. а) 2x2 + 9x – 10 = 0; б) 5x2 + 12x + 7 = 0; в) 19x2 – 23x + 5 = 0; г) Зx2 + 113x – 7 = 0.
Задание № 32.4. а) x2 – 9 = 0; б) 2x2 + 3x = 0; в) x2 + 5x = 0; г) 7x2 – 1 = 0.
Задание № 32.5. а) 0,2x2 – 4x – 1 = 0; б) √3x2 – 12x – 7√3 = 0; в) x2 – √5x +1 = 0; г) 2/3 • x2 + 2x – 1 = 0.
Не используя формулу корней, найдите корни квадратного уравнения:
Задание № 32.6. а) x2 + 3x + 2 = 0; б) x2 – 15x + 14 = 0; в) x2 + 8x + 7 = 0; г) x2 – 19x + 18 = 0.
Задание № 32.7. а) x2 + 3x – 4 = 0; б) x2 – 10x – 11 = 0; в) x2 – 9x – 10 = 0; г) x2 + 8x – 9 = 0.
Задание № 32.8. а) x2 + 9x + 20 = 0; б) x2 – 15x + 36 = 0; в) x2 + 5x – 14 = 0; г) x2 – 7x – 30 = 0.
Задание № 32.9. Составьте квадратное уравнение, корнями которого являются числа:
а) x1 = 4; x2 = 2; б) x1 = 3; x2 = –5; в) x1 = –8; x2 = 1; г) x1 = –6; x2 = –2.
Задание № 32.10. Составьте квадратное уравнение, корнями которого являются числа:
а) x1 = 2,5; x2 = –2; б) x1 = –2/3; x2 = –1 1/2; в) x1 = –2,4; x2 = –1,5; г) x1 = 3/5; х2 = –1 2/3.
Задание № 32.11. Может ли квадратное уравнение x2 + bх – 8 = 0:
а) не иметь корней;
б) иметь равные корни;
в) иметь два различных корня разных знаков;
г) иметь два различных корня одного и того же знака?
Задание № 32.12. Пусть х1 и x2 – корни квадратного уравнения аx2 + bх + с = 0. Найдите:
а) b и с, если а = 2, х1 = 3, x2 = –0,5;
б) а и с, если b = –1, х1 = 3, x2 = –4;
в) а и b, если с = 4, х1 = –2, x2 = –0,25;
г) а и с, если b = 6, х1 = 3, x2 = –4.
Задание № 32.13. При каких значениях параметра р сумма корней квадратного уравнения x2 + (р2 + 4р – 5)х – р = 0 равна нулю?
Задание № 32.14. При каких значениях параметра р произведение корней квадратного уравнения x2 + 3х + (р2 – 7р + 12) = 0 равно нулю?
Задание № 32.15.
Задание № 32.16.
Задание № 32.17.
Задание № 32.18.
Задание № 32.19.
Задание № 32.20.
Задание № 32.21.
Задание № 32.22.
Задание № 32.23.
Задание № 32.24.
Задание № 32.25.
Задание № 32.26.
Задание № 32.27.
Задание № 32.28.
Задание № 32.29.
Задание № 32.30.
Задание № 32.31.
Задание № 32.32.
Задание № 32.33.
Задание № 32.34.
Задание № 32.35.
Задание № 32.36.
Задание № 32.37.
Задание № 32.38.
Задание № 32.39.
Задание № 32.40.
Задание № 32.41.
Задание № 32.42.
Задание № 32.43.
Задание № 32.44.
Задание № 32.45.
Задание № 32.46.
Задание № 32.47.
Задание № 32.48.
Задание № 32.49.
Задание № 32.50.
Задание № 32.51.
Задание № 32.52.
Задание № 32.53.
Задание № 32.54.
Задание № 32.55.
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. § 32. Теорема Виета и её применения. ОТВЕТЫ на упражнения 32.1 — 32.55. Вернуться в ОГЛАВЛЕНИЕ.
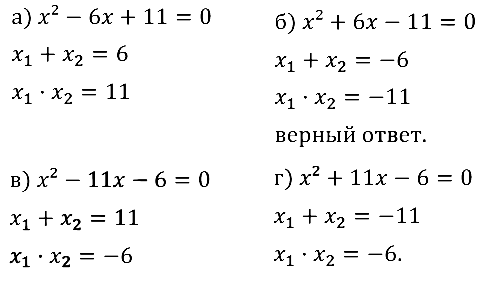
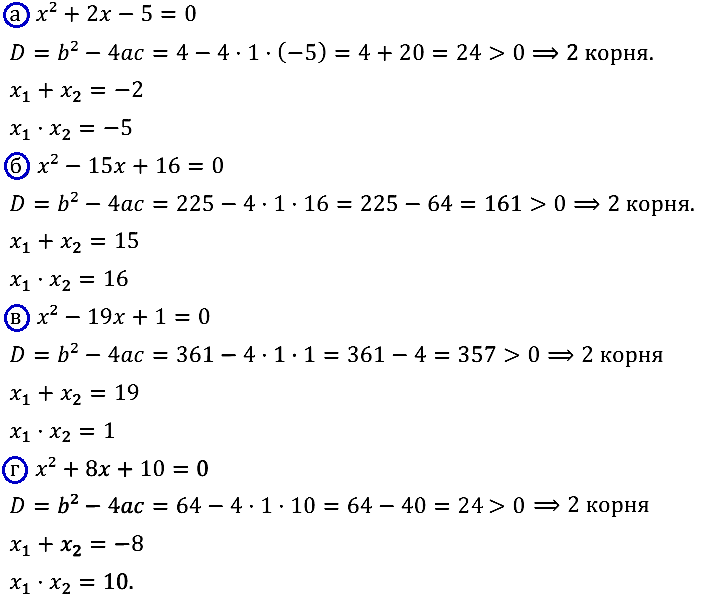

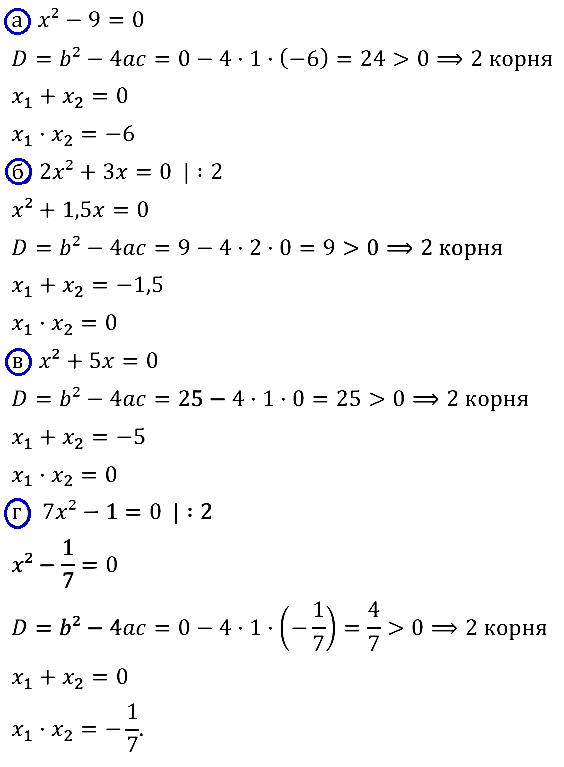

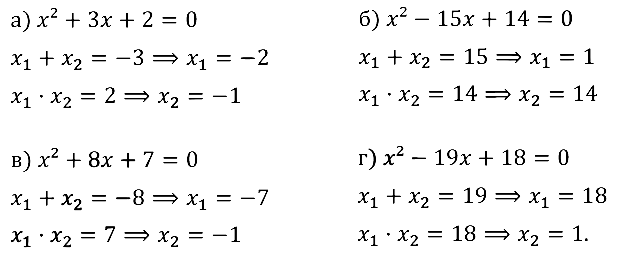
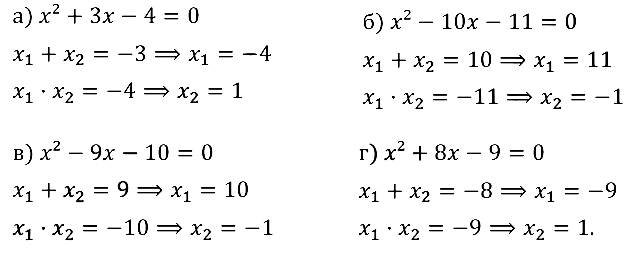
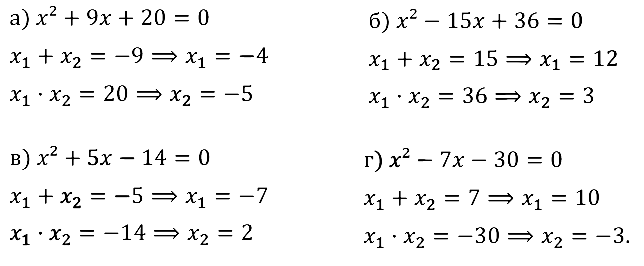
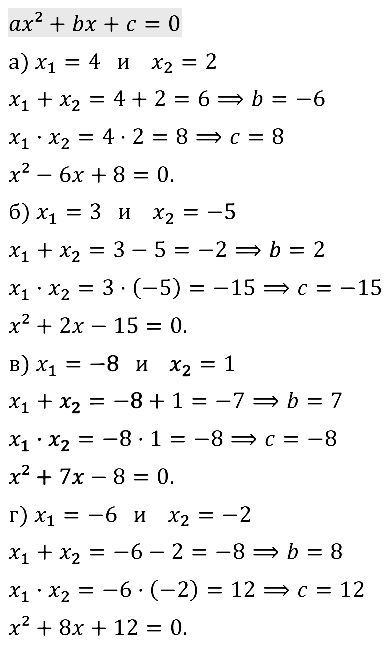
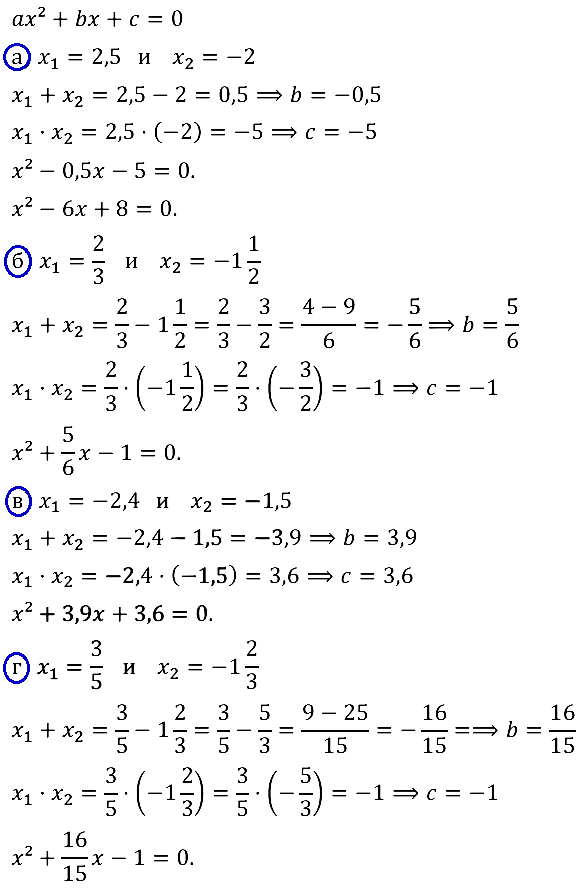

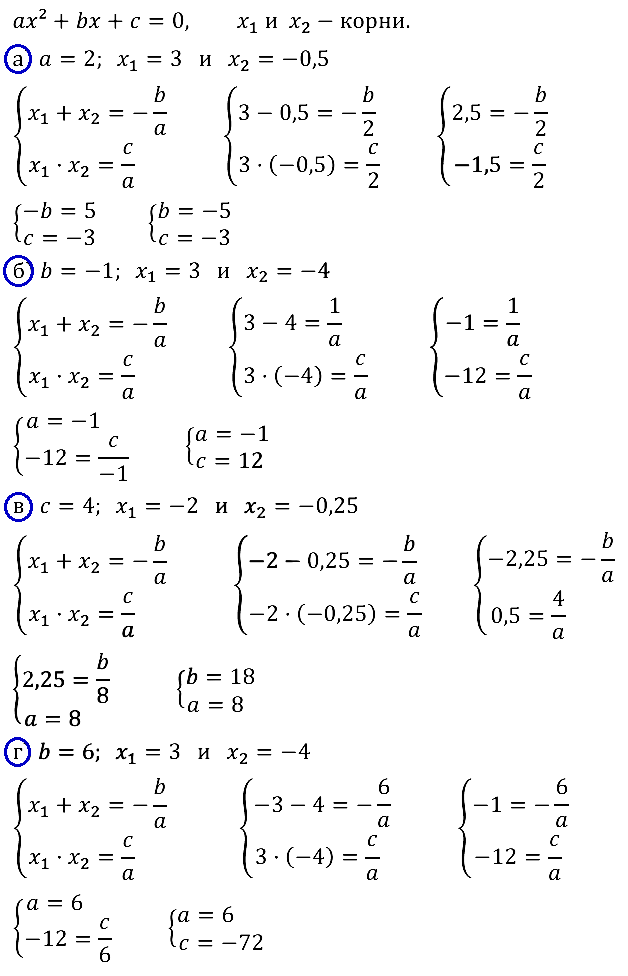
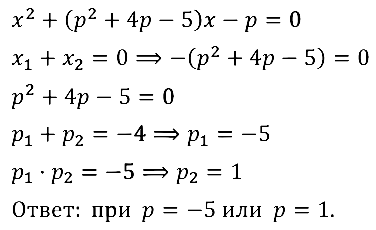
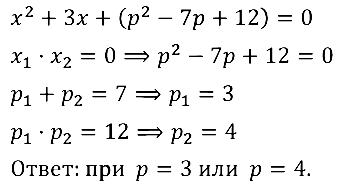
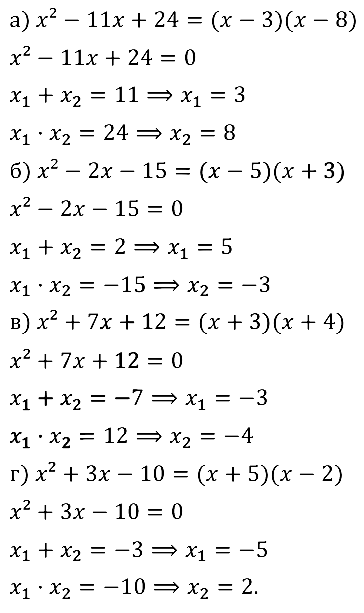















Номера упражнений перепутаны