Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Теорема Пифагора». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Теорема Пифагора
Вариант 1
- Найдите гипотенузу прямоугольного треугольника, если его катеты равны 6 см и 8 см.
- Найдите катет прямоугольного треугольника, если его гипотенуза и второй катет соответственно равны 8 см и 4 см.
- Сторона квадрата равна 3√2 см. Найдите его диагональ.
- Диагональ прямоугольника равна 34 см. Найдите стороны прямоугольника, если их длины относятся как 15 : 8.
- Боковая сторона равнобедренного треугольника равна 7 см, а основание — 6 см. Найдите высоту треугольника, проведённую к основанию.
- Сторона ромба равна 13 см, а одна из его диагоналей — 10 см. Найдите вторую диагональ ромба.
- Две стороны прямоугольного треугольника равны 5 см и 8 см. Найдите третью сторону треугольника. Сколько решений имеет задача?
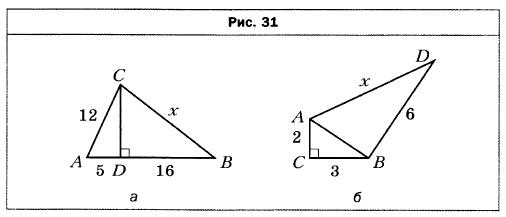
- Найдите длину неизвестного отрезка х на рисунке 31 (длины отрезков даны в сантиметрах).
- Диагональ равнобокой трапеции равна 17 см, а высота — 8 см. Найдите среднюю линию трапеции.
- В равнобокой трапеции ABCD высота BE делит основание AD на отрезки длиной 5 см и 16 см. Найдите диагональ трапеции, если её боковая сторона равна 13 см.
- Катеты прямоугольного треугольника относятся как 3 : 4, а его гипотенуза равна 20 см. Найдите катеты треугольника.
- Боковая сторона равнобедренного треугольника относится к высоте, проведённой к основанию, как 5 : 3. Найдите стороны треугольника, если его периметр равен 36 см.
- Катет прямоугольного треугольника равен 6 см, а медиана, проведённая к нему, — 5 см. Найдите гипотенузу треугольника.
- В треугольнике ABС известно, что АВ = 10 см, ВС = 15 см, а высота BD равна 8 см. Найдите сторону АС треугольника. Сколько решений имеет задача?
- В равнобедренном треугольнике АВС (АВ = ВС) проведена высота AD. Известно, что BD = 4 см, DC = 16 см. Найдите основание АС треугольника. Сколько решений имеет задача?
- Из точки к прямой проведены две наклонные. Длина одной из них равна 25 см, а длина её проекции на эту прямую — 15 см. Найдите длину второй наклонной, если она образует с прямой угол 30°.
- Из точки к прямой проведены две наклонные, проекции которых на эту прямую равны 5 см и 9 см. Найдите расстояние от точки до данной прямой, если разность наклонных равна 2 см.
- В равнобокую трапецию вписана окружность, радиус которой равен 12 см. Найдите основания трапеции, если её боковая сторона равна 25 см.
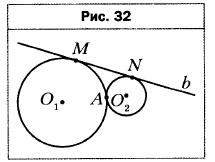
- Две окружности, радиусы которых равны 9 см и 4 см, имеют одну общую точку А (рис. 32). Прямая b касается этих окружностей в точках М и N. Найдите отрезок MN.
- Точки М и N лежат в разных полуплоскостях относительно прямой а. Из этих точек к прямой а проведены перпендикуляры МК и NF. Найдите отрезок KF, если МК = 3 см, NF = 2 см, MN = 13 см.
- Биссектриса острого угла прямоугольного треугольника делит один из катетов на отрезки длиной 25 см и 20 см. Найдите периметр треугольника.
- Постройте отрезок х, если
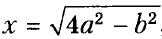 , где а и b — длины данных отрезков (а > b).
, где а и b — длины данных отрезков (а > b).
Вариант 2
- Найдите гипотенузу прямоугольного треугольника, если его катеты равны 5 см и 12 см.
- Найдите катет прямоугольного треугольника, если его гипотенуза и второй катет соответственно равны 9 см и 5 см.
- Сторона квадрата равна 4√2 см. Найдите его диагональ.
- Одна из сторон прямоугольника равна 16 см. Найдите вторую сторону прямоугольника и его диагональ, если их длины относятся как 3 : 5.
- Боковая сторона равнобедренного треугольника равна 12 см, а высота, проведённая к основанию, — 7 см. Найдите основание треугольника.
- Диагонали ромба равны 14 см и 48 см. Найдите сторону ромба.
- Две стороны прямоугольного треугольника равны 4 см и 7 см. Найдите третью сторону треугольника. Сколько решений имеет задача?
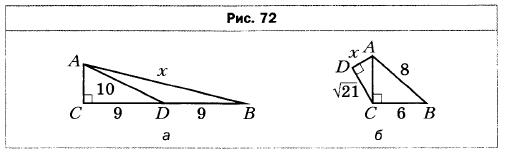
- Найдите длину неизвестного отрезка х на рисунке 72 (длины отрезков даны в сантиметрах).
- Высота равнобокой трапеции равна 9 см, а средняя линия — 12 см. Найдите диагональ трапеции.
- В параллелограмме ABCD высота BE делит сторону AD на отрезки АЕ = 8 см и ED = 20 см. Найдите диагональ BD параллелограмма, если его сторона АВ равна 17 см.
- Гипотенуза и один из катетов прямоугольного треугольника относятся как 13 : 12, а второй катет равен 15 см. Найдите неизвестные стороны треугольника.
- Основание равнобедренного треугольника относится к проведённой к нему высоте как 8:3. Найдите стороны треугольника, если его периметр равен 72 см.
- Катет прямоугольного треугольника равен 5 см, а медиана, проведённая к другому катету, — 13 см. Найдите гипотенузу треугольника.
- В треугольнике АВС известно, что АС = 13 см, АВ = 15 см, а высота АЕ равна 12 см. Найдите сторону ВС треугольника. Сколько решений имеет задача?
- В равнобедренном треугольнике АВС (АС = ВС) проведена высота BE. Известно, что СЕ = 1 см, АЕ = 24 см. Найдите основание АВ треугольника. Сколько решений имеет задача?
- Из точки к прямой проведены две наклонные. Длина одной из них равна 15 см, а её проекция на эту прямую — 12 см. Найдите длину второй наклонной, если она образует с прямой угол 45°.
- Из точки к прямой проведены две наклонные, длины которых равны 5 см и 7 см. Найдите расстояние от точки до данной прямой, если разность проекций наклонных на эту прямую равна 4 см.
- В равнобокую трапецию вписана окружность, радиус которой равен 8 см. Найдите основания трапеции, если их разность равна 24 см.
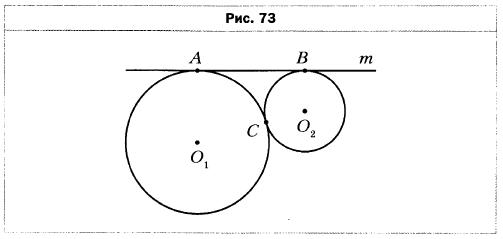
- Две окружности, радиусы которых равны 16 см и 9 см, имеют одну общую точку С (рис. 73). Прямая m касается этих окружностей в точках А к В. Найдите отрезок АВ.
- Точки С и D лежат в разных полуплоскостях относительно прямой b. Из этих точек к прямой b проведены перпендикуляры СЕ и DF. Найдите отрезок CD, если СЕ = 1 см, DF = 7 см, ЕF = 15 см.
- Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 15 см и 20 см. Найдите периметр треугольника.
- Постройте отрезок х, если
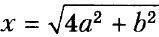 , где а и b — длины данных отрезков.
, где а и b — длины данных отрезков.
Вариант 3
- Найдите гипотенузу прямоугольного треугольника, если его катеты равны 10 см и 24 см.
- Найдите катет прямоугольного треугольника, если его гипотенуза и второй катет соответственно равны 8 см и 2 см.
- Сторона квадрата равна 5√2 см. Найдите его диагональ.
- Диагональ прямоугольника равна 50 см. Найдите стороны прямоугольника, если их длины относятся как 7 : 24.
- Основание равнобедренного треугольника равно 10 см, а высота, проведённая к основанию, — 8 см. Найдите боковую сторону треугольника.
- Сторона ромба равна 17 см, а одна из его диагоналей — 16 см. Найдите вторую диагональ ромба.
- Две стороны прямоугольного треугольника равны 7 см и 10 см. Найдите третью сторону треугольника. Сколько решений имеет задача?
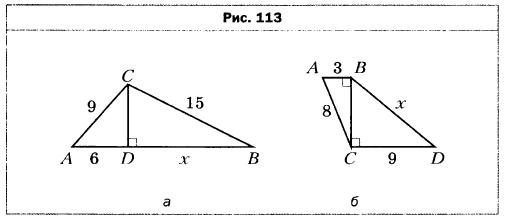
- Найдите длину неизвестного отрезка х на рисунке 113 (длины отрезков даны в сантиметрах).
- Диагональ равнобокой трапеции равна 15 см, а средняя линия — 4 см. Найдите высоту трапеции.
- В равнобокой трапеции ABCD боковая сторона равна 10 см, а высота BF делит основание AD на отрезки, меньший из которых равен 6 см. Найдите большее основание трапеции, если её диагональ равна 17 см.
- Катеты прямоугольного треугольника относятся как 12 : 5, а гипотенуза равна 39 см. Найдите катеты треугольника.
- Боковая сторона равнобедренного треугольника относится к высоте, проведённой к основанию, как 5 : 4. Найдите стороны треугольника, если его периметр равен 48 см.
- Гипотенуза прямоугольного треугольника равна 25 см, а один из катетов — 7 см. Найдите медиану треугольника, проведённую к другому катету.
- В треугольнике АВС известно, что АС = 13 см, ВС = = 20 см, а высота CD равна 12 см. Найдите сторону АВ треугольника. Сколько решений имеет задача?
- В равнобедренном треугольнике АВС (АВ = АС) проведена высота СН. Известно, что АН = 5 см, ВН = 15 см. Найдите основание ВС треугольника. Сколько решений имеет задача?
- Из точки к прямой проведены две наклонные. Одна из них образует с прямой угол 45°, а её проекция на эту прямую равна 11√2 см. Найдите длину второй наклонной, если её проекция на эту прямую равна √82 см.
- Из точки к прямой проведены две наклонные, проекции которых на эту прямую равны 3 см и 7 см. Найдите расстояние от точки до данной прямой, если сумма наклонных равна 28 см.
- В равнобокую трапецию вписана окружность. Найдите радиус этой окружности, если сумма оснований трапеции равна 50 см, а разность оснований — 14 см.
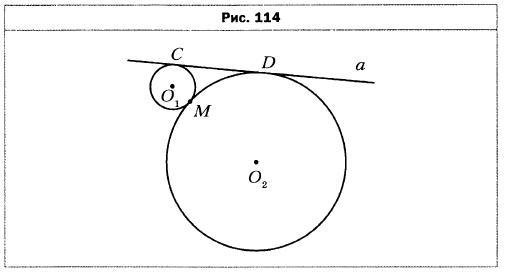
- Две окружности, радиусы которых равны 2 см и 8 см, имеют одну общую точку М (рис. 114). Прямая а касается этих окружностей в точках С и D. Найдите отрезок CD.
- Точки А и В лежат в разных полуплоскостях относительно прямой m. Из этих точек к прямой m проведены перпендикуляры АС и BD. Найдите отрезок CD, если АС = 3 см, BD = 9 см, АВ = 15 см.
- Биссектриса острого угла прямоугольного треугольника делит один из катетов на отрезки длиной 15 см и 25 см. Найдите периметр треугольника.
- Постройте отрезок х, если
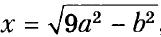 , где а и b — длины данных отрезков (а > b).
, где а и b — длины данных отрезков (а > b).
Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Теорема Пифагора». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!