Алгебра 8 класс. Мерзляк, Поляков (угл.) 2019
О Г Л А В Л Е Н И Е Вернуться к списку тем учебника
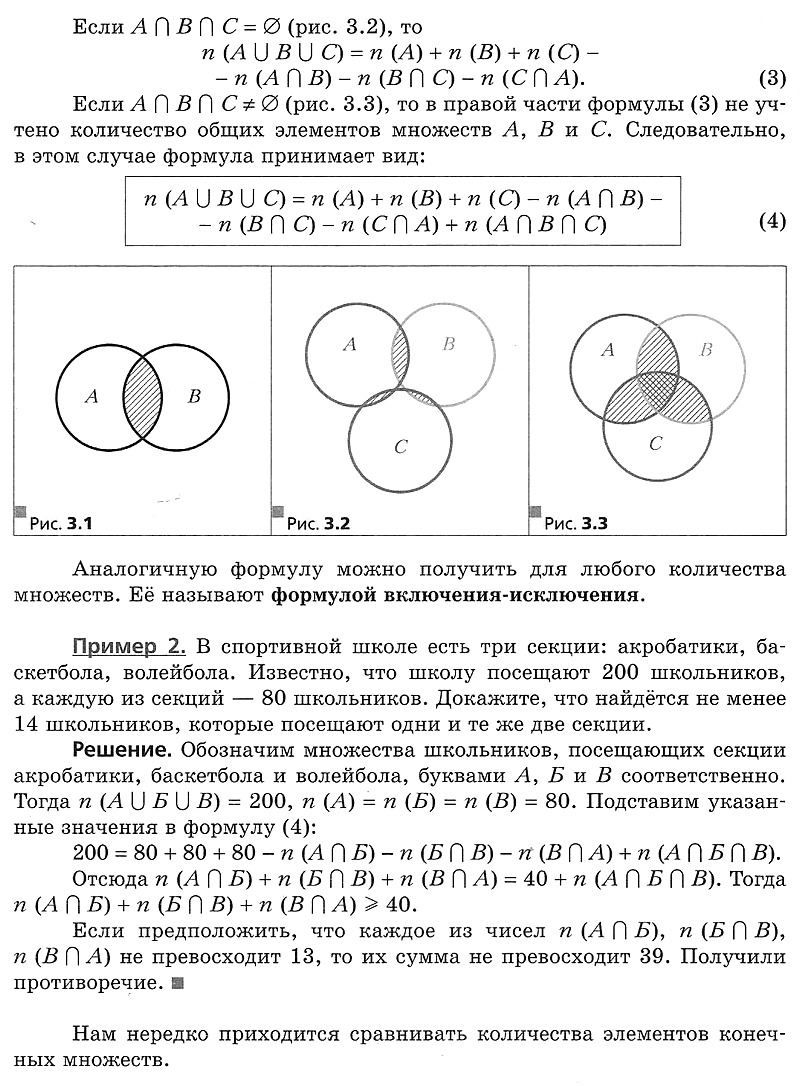
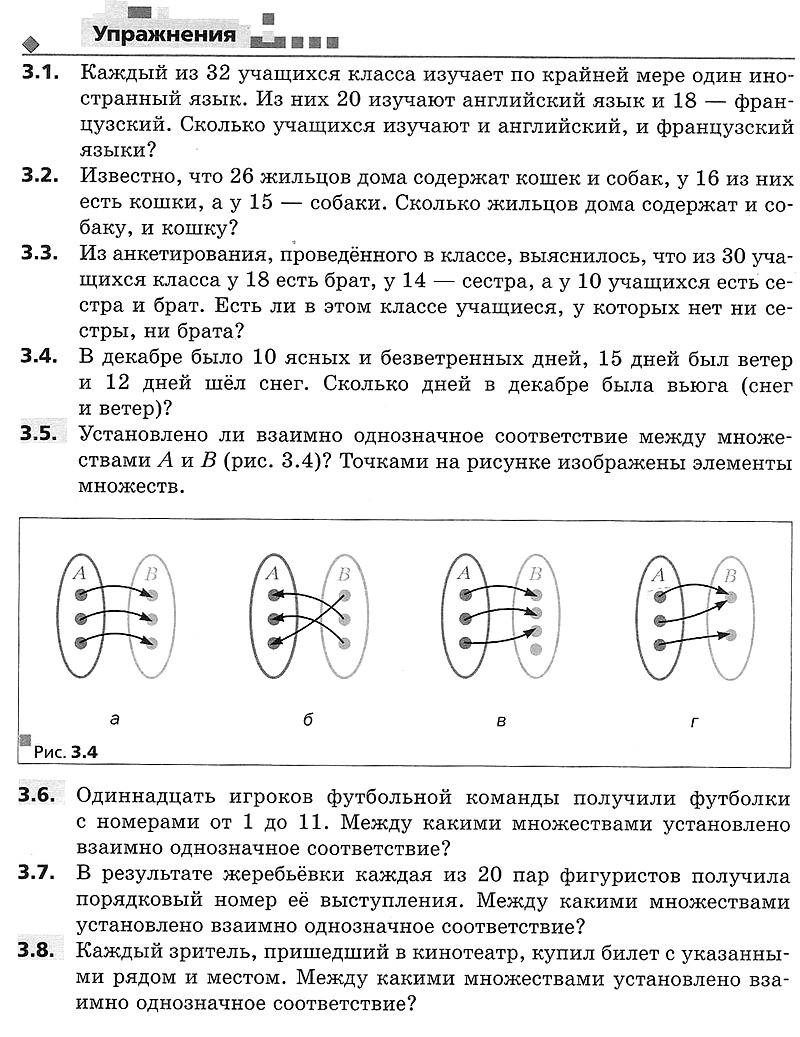
§ 3. Формула включения-исключения.
Взаимно однозначное соответствие
О Г Л А В Л Е Н И Е Вернуться к списку тем учебника
Ознакомительная версия для принятия решения о покупке книги: Мерзляк, Поляков: Алгебра. Углубленный уровень: 8 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). § 3. Формула включения–исключения. Взаимно однозначное соответствие.