Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2022). § 28. Формулы корней квадратных уравнений. ОТВЕТЫ на упражнения 28.1 — 28.48. ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 28.1 — 28.48)
§ 28. Формулы корней квадратных уравнений
Найдите дискриминант квадратного уравнения:
Задание № 28.1. а) х2 + 5х – 6 = 0; б) х2 – 1,3х + 2 = 0; в) х2 – 7х – 4 = 0; г) х2 – 2,4х +1 = 0.
Задание № 28.2. а) 3х2 + 2х – 1 = 0; б) –х2 + 4х + 3 = 0; в) 4х2 – 5х – 4 = 0; г) –2х2 + 5х + 3 = 0.
Определите число корней квадратного уравнения:
Задание № 28.3. а) х2 – 8х – 84 = 0; б) 36х2 – 12х + 1 = 0; в) х2 – 22х – 23 = 0; г) 16х2 – 8х + 1 = 0.
Задание № 28.4. а) х2 + 3х + 24 = 0; б) х2 – 16х + 64 = 0; в) х2 – 2х + 5 = 0; г) х2 + 6х + 9 = 0.
Задание № 28.5. а) х2 – 5х + 6 = 0; б) х2 – 2х – 15 = 0; в) х2 + 6x + 8 = 0; г) x2 – 3x – 18 = 0.
Задание № 28.6. а) х2 + 42х + 441 = 0; б) х2 + 8х + 7 = 0; в) х2 – 34х + 289 = 0; г) х2 + 4х – 5 = 0.
Задание № 28.7. а) 2х2 + 3х + 1 = 0; б) 3х2 – 3х + 4 = 0; в) 5х2 – 8х + 3 = 0; г) 14х2 + 5х – 1 = 0.
Задание № 28.8. а) 4х2 + 10х – 6 = 0; б) 25х2 + 10х + 1 = 0; в) 3х2 – 8х + 5 = 0; г) 4х2 + х + 67 = 0.
Задание № 28.9.
Задание № 28.10.
Задание № 28.11.
Задание № 28.12.
Задание № 28.13.
Задание № 28.14.
Задание № 28.15.
Задание № 28.16.
Задание № 28.17.
Задание № 28.18.
Задание № 28.19.
Задание № 28.20.
Задание № 28.21. Докажите, что при любом значении параметра р уравнение 3х2 – рх – 2 = 0 имеет два корня.
Задание № 28.22. Найдите натуральное число, квадрат которого на 56 больше самого числа.
Задание № 28.23. Одна сторона прямоугольника на 5 см больше другой, а его площадь равна 84 см2. Найдите стороны прямоугольника.
Задание № 28.24. Представьте число 120 в виде произведения двух чисел, одно из которых на 2 меньше другого.
Задание № 28.25. Площадь прямоугольного треугольника равна 180 м2. Найдите катеты этого треугольника, если один больше другого на 31 м.
Задание № 28.26. От квадратного листа картона отрезали полоску шириной 3 см. Площадь оставшейся части равна 70 см2. Найдите первоначальные размеры листа картона.
Задание № 28.27. Произведение двух последовательных натуральных чисел на 271 больше их суммы. Найдите эти числа.
Задание № 28.28. Сумма квадратов двух последовательных натуральных чисел равна 1201. Чему равна разность квадратов этих чисел?
Задание № 28.29. Найдите три последовательных натуральных числа, сумма квадратов которых равна 1589.
Задание № 28.30. Гипотенуза прямоугольного треугольника больше одного из катетов на 32 см и больше другого на 9 см. Найдите стороны треугольника.
Задание № 28.31. В прямоугольном треугольнике один катет меньше гипотенузы на 8 см, а другой – на 4 см. Найдите гипотенузу.
Задание № 28.32. Сумма квадратов двух последовательных натуральных чисел больше их произведения на 307. Найдите эти числа.
Задание № 28.33. Квадрат суммы двух последовательных натуральных чисел больше суммы их квадратов на 840. Найдите эти числа.
Задание № 28.34. Вкладчик положил в банк 10 000 р. под некоторый процент годовых. В конце первого года банк увеличил процент годовых на 5%. Под какой процент были положены деньги, если после двух лет хранения денег в банке вкладчик получил 11 550 рублей?
Задание № 28.35. Завод выпускал миксеры по цене 2500 рублей за штуку. Предполагалось, что при постепенном внедрении новой технологии производства стоимость изделия ежемесячно будет уменьшаться на один и тот же процент в течение нескольких месяцев. Однако оказалось, что за второй месяц стоимость изделия снизилась на 10% больше, чем предполагалось. На сколько процентов предполагалось снижать стоимость миксера, если после двух месяцев его цена составила 1800 рублей?
Задание № 28.36.
Задание № 28.37.
Задание № 28.38.
Задание № 28.39.
Задание № 28.40.
Задание № 28.41.
Задание № 28.42.
Задание № 28.43.
Задание № 28.44.
Задание № 28.45.
Задание № 28.46.
Задание № 28.47.
Задание № 28.48.
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. § 28. Формулы корней квадратных уравнений. ОТВЕТЫ на упражнения 28.1 — 28.48. Вернуться в ОГЛАВЛЕНИЕ.
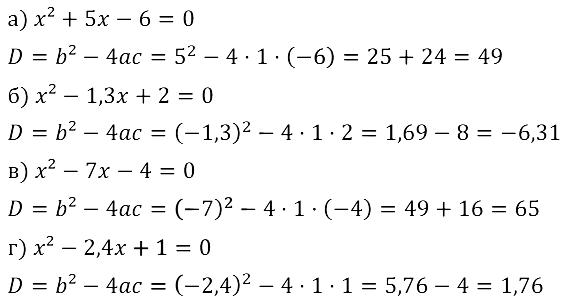
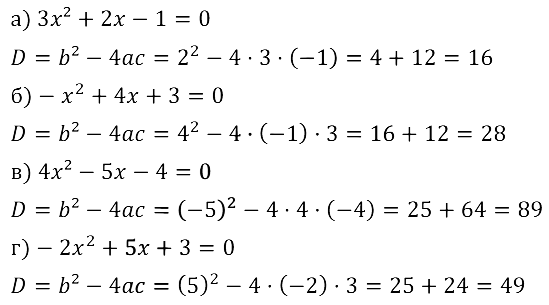
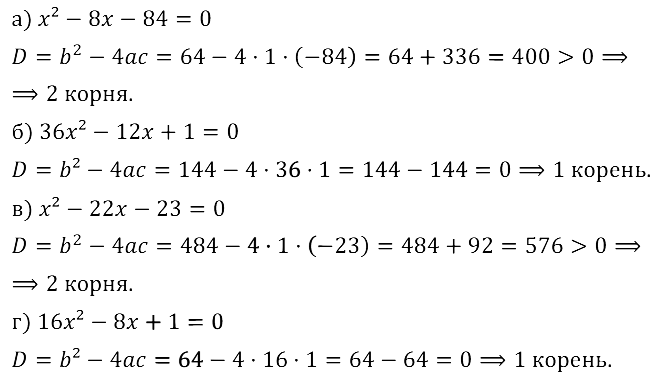
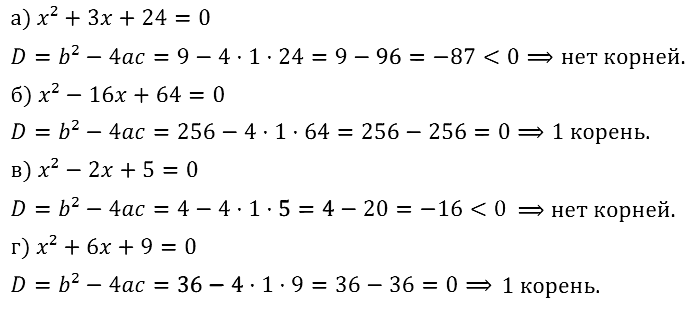
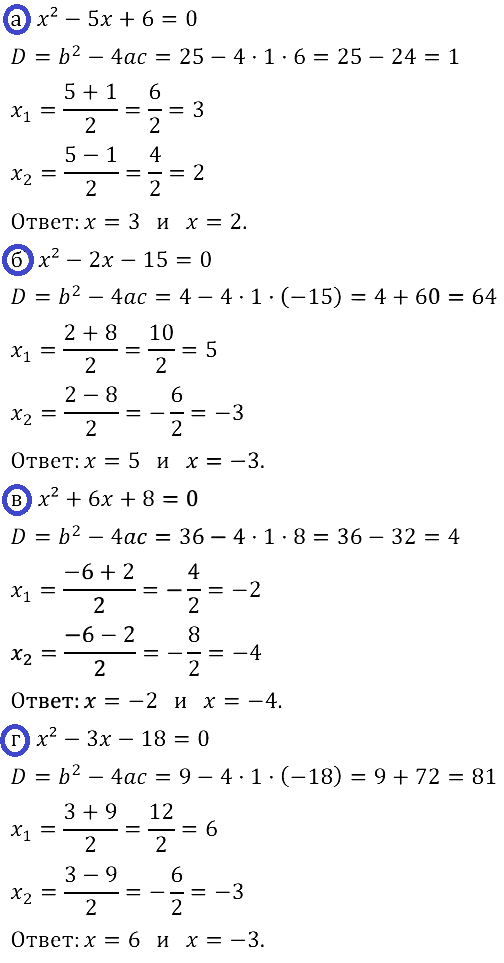

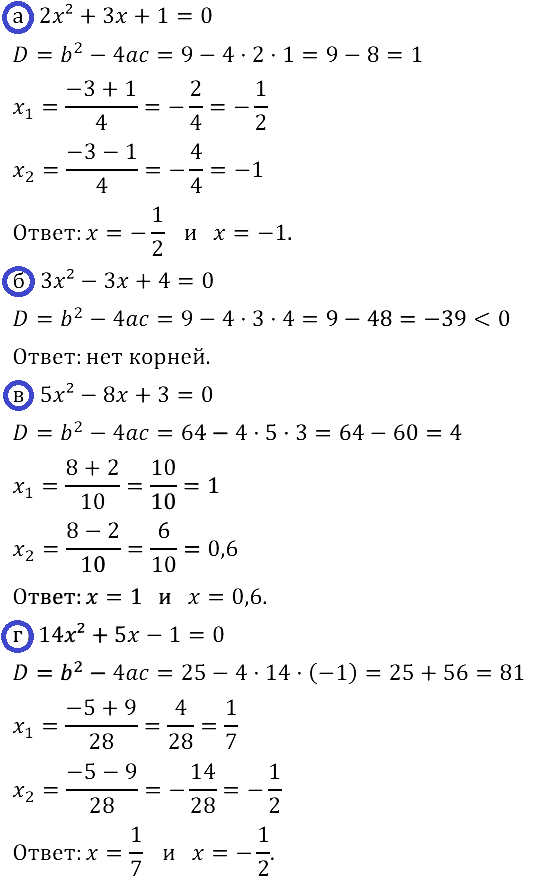
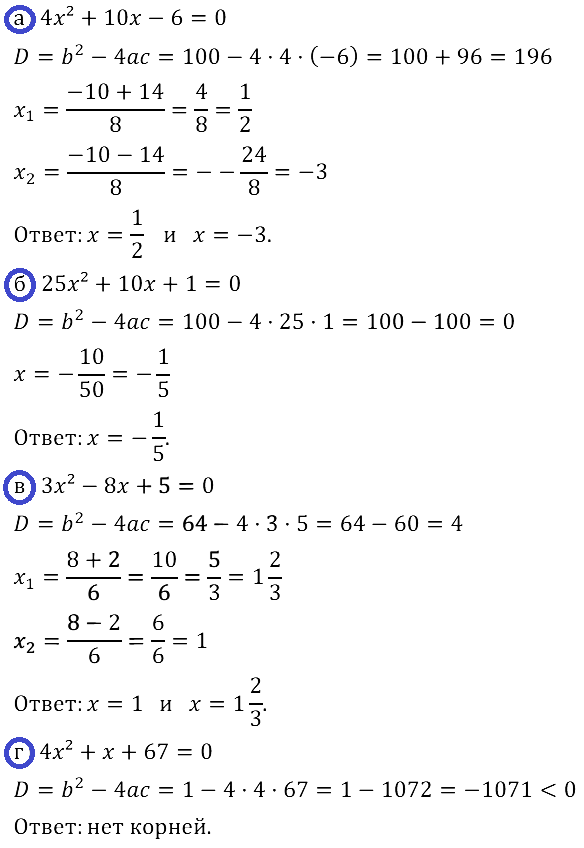
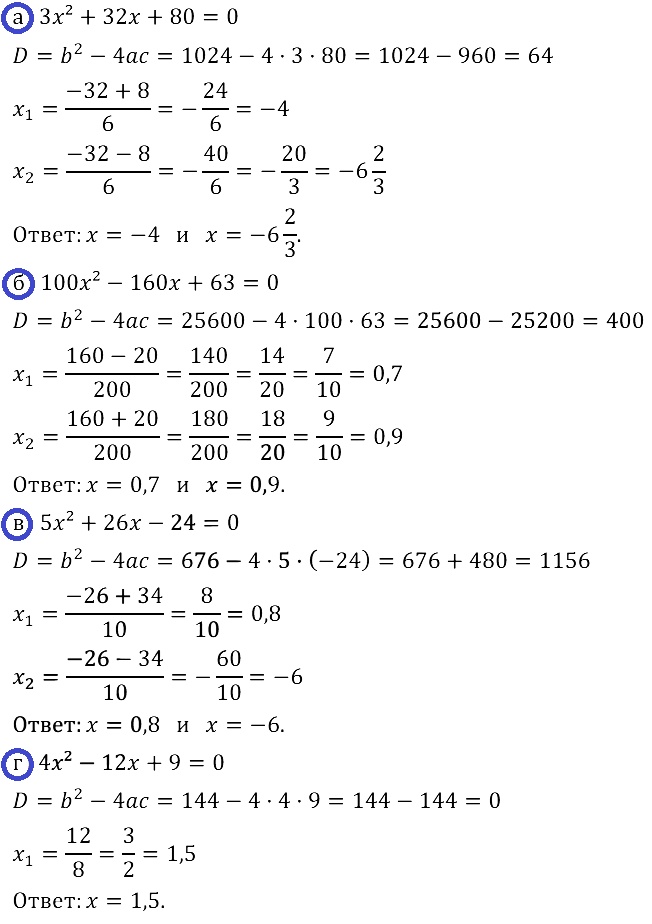

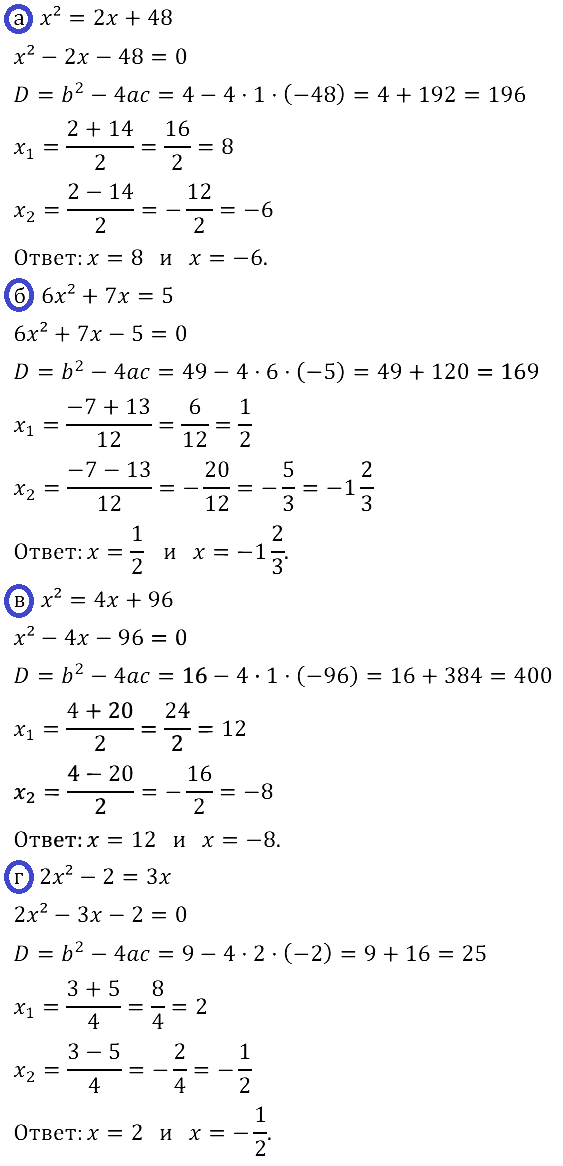
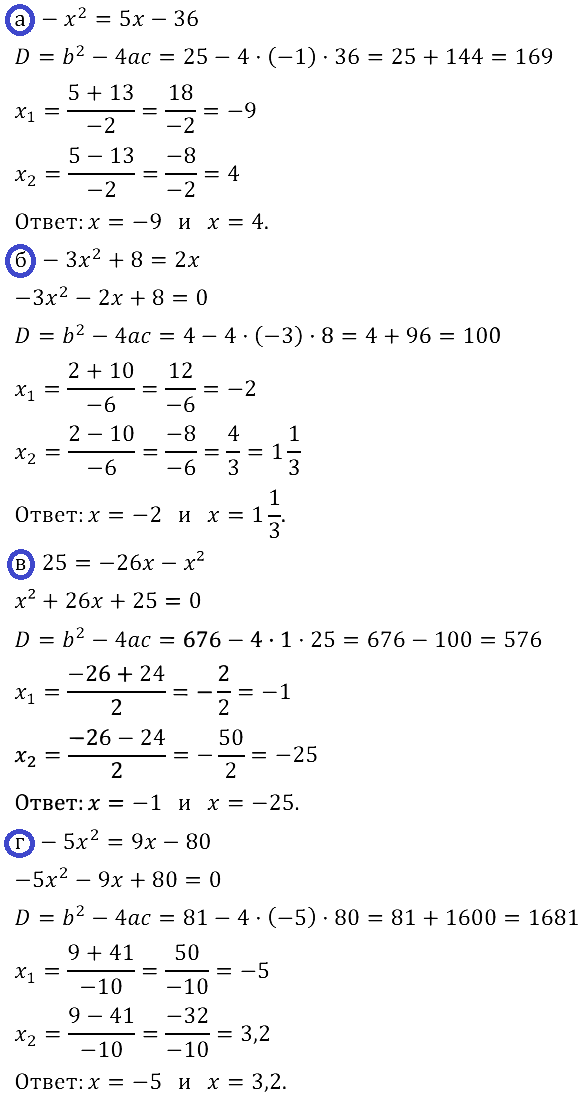
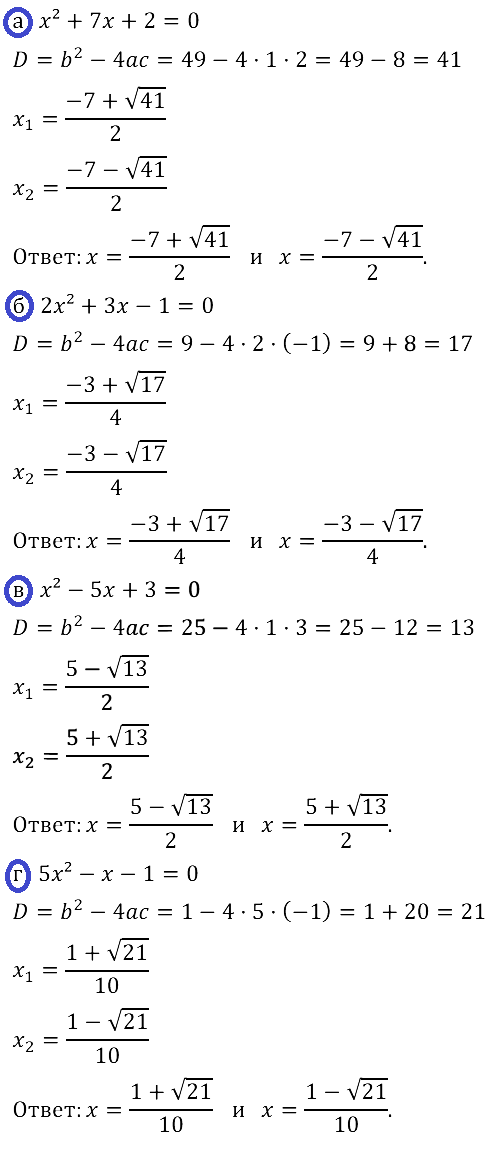


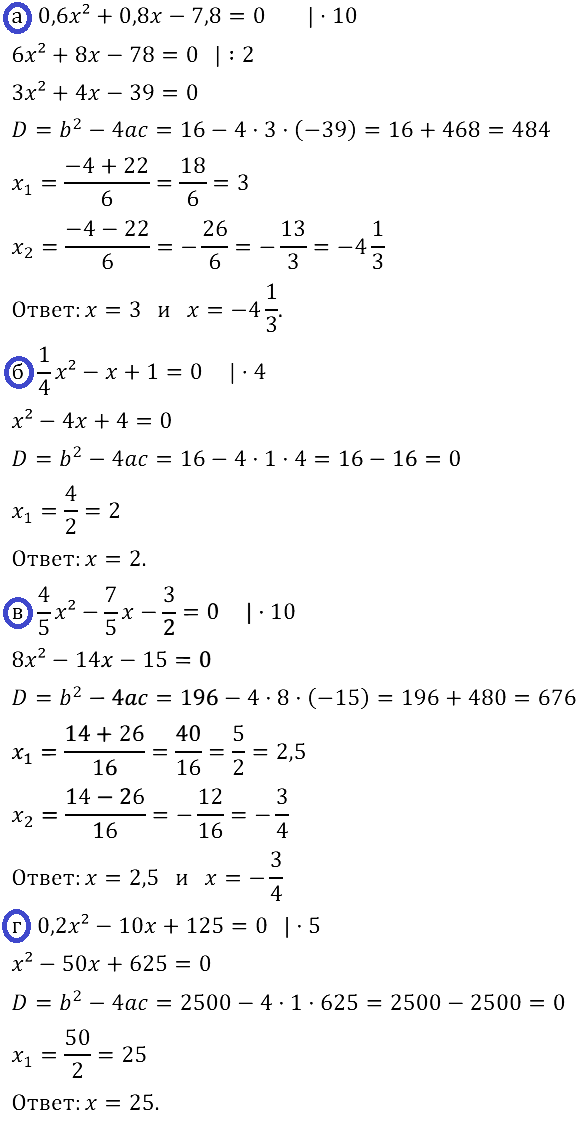
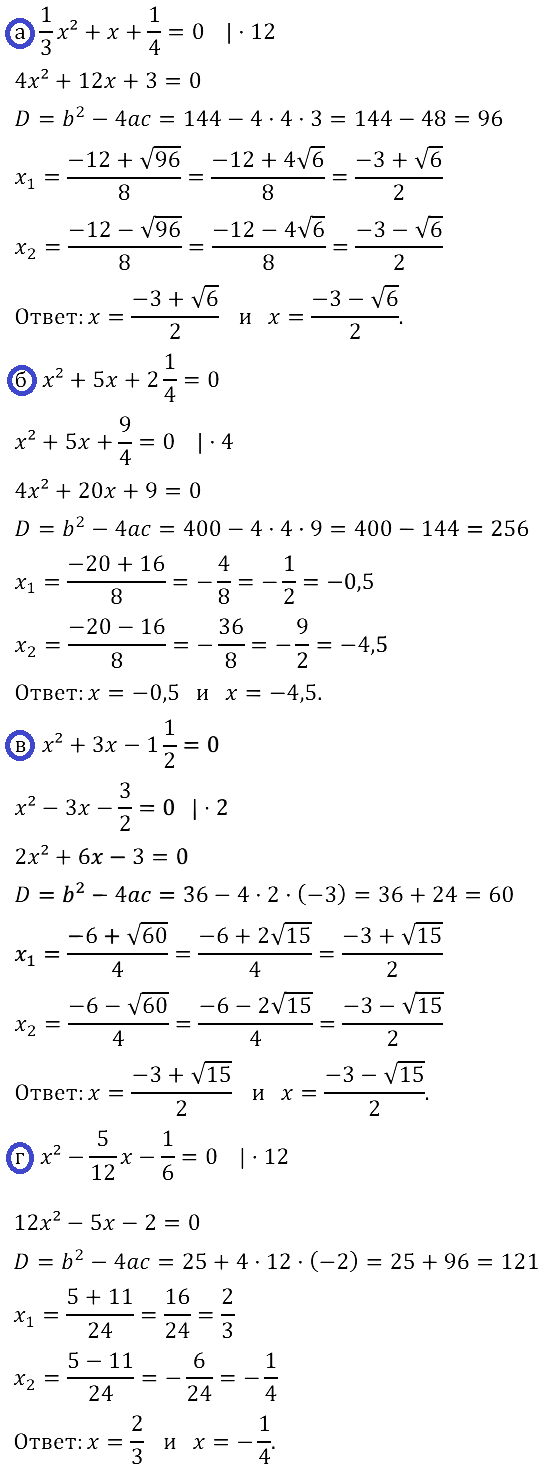



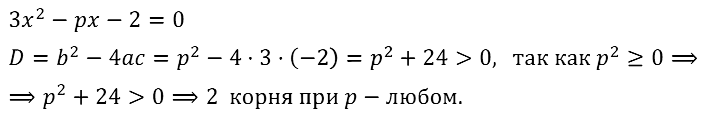














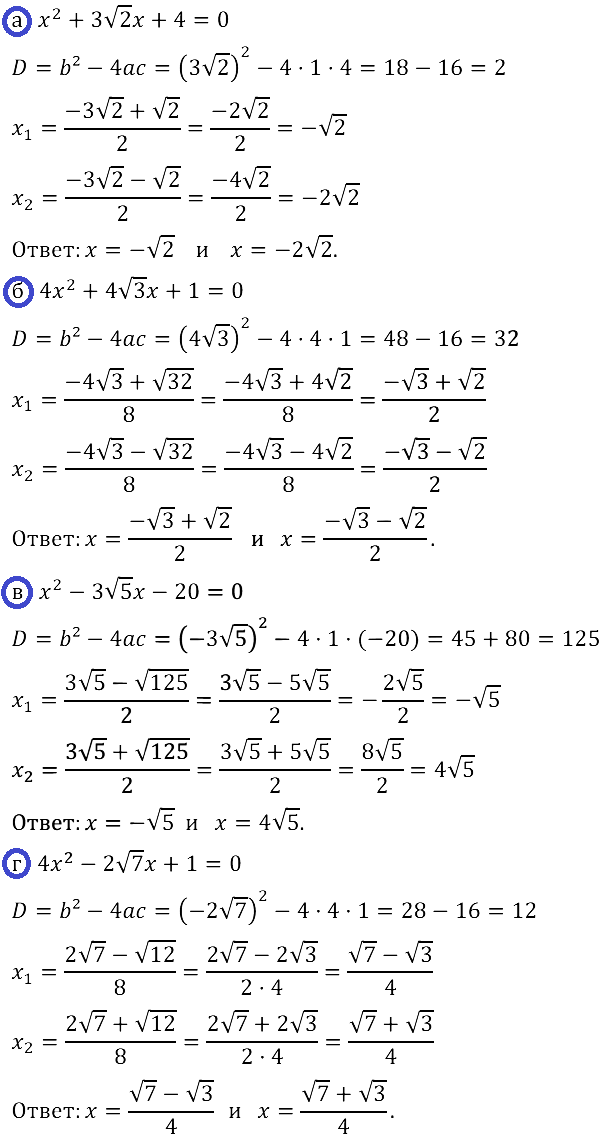
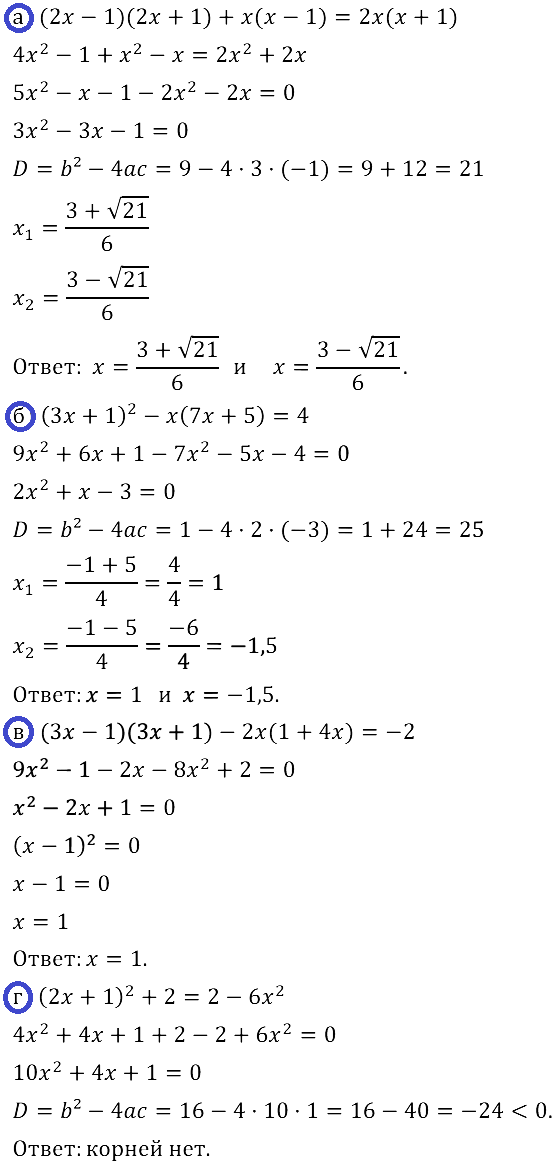








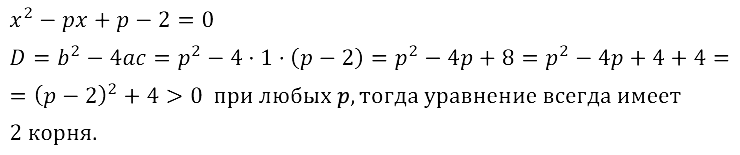

Есть ошибка в номере 28.11
Перепроверили, ошибок нет.
Ошибка в номере 28.19 (в). Дискриминант равен 1156
Исправлено. Спасибо.