Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). § 34. Комбинаторные и вероятностные задачи к главе 4. ОТВЕТЫ на упражнения 34.1 — 34.7. ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 34.1 — 34.7)
§ 34. Комбинаторные и вероятностные задачи к главе 4.
Задание № 34.1. Для контрольной работы составляют различные квадратные уравнения вида x2 + bx + c = 0. Коэффициент b произвольно выбирают из чисел –2, –4, –6, а коэффициент с – из чисел 4, 9.
а) Нарисуйте дерево вариантов составления таких квадратных уравнений.
б) Сколько всего таких уравнений можно составить?
в) Сколько среди них уравнений, дискриминант которых равен нулю?
г) Сколько среди них уравнений^ которые имеют хотя бы один корень?
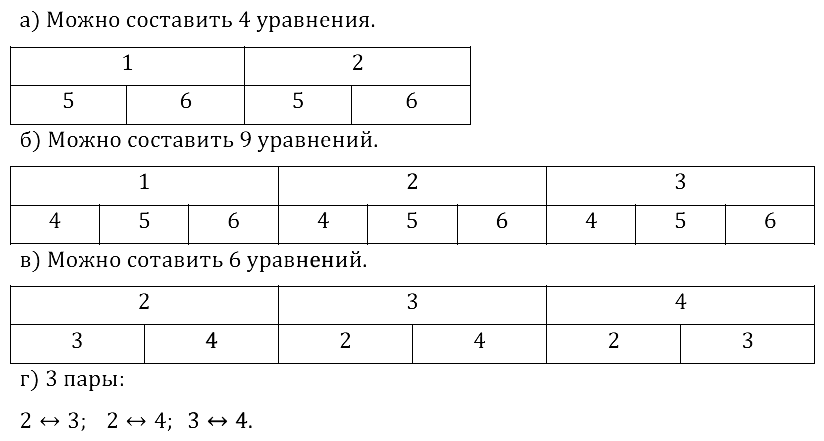
Задание № 34.2. Для составления квадратного уравнения с заранее заданными корнями х1 и х2 поступают так. Сначала составляют произведение (х – х1)(х – х2). Затем раскрывают скобки и приводят подобные члены. Полученный квадратный трёхчлен приравнивают нулю. Сколько различных квадратных уравнений можно составить таким образом, выбирая:
а) корень х1 из чисел 1, 2, а корень х2 из чисел 5, 6;
б) корень х1 из чисел 1, 2, 3, а корень х2 из чисел 4, 5, 6;
в) оба корня из чисел 2, 3, 4, если совпадение корней допустимо;
г) оба корня из чисел 2, 3, 4, если корни должны быть различными?
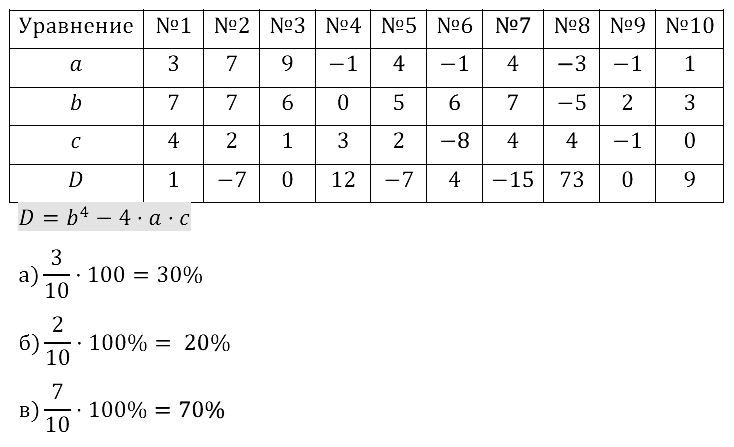
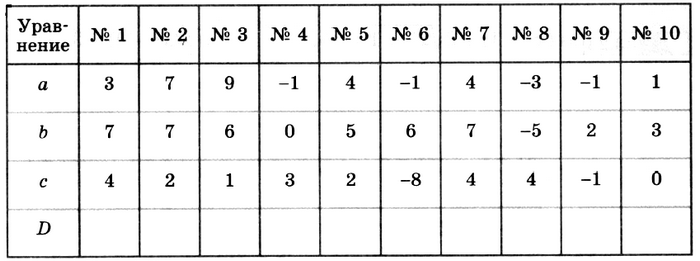
Задание № 34.3. Заполните таблицу значений дискриминанта для уравнений вида ах2 + bх + с = 0:
Какова процентная частота уравнений:
а) не имеющих корней;
б) имеющих единственный корень;
в) имеющих хотя бы один корень?
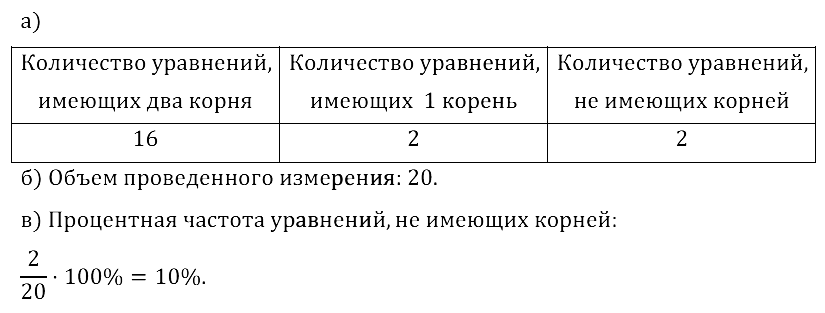
Задание № 34.4. a) Откройте задачник на с. 161. В каждом из заданий 28.6–28.10 определите количество корней квадратного уравнения. Результаты поочерёдно внесите во вторую строку таблицы и подведите в ней же числовой итог.
| Кол-во уравнений, имеющих 2 корня | Кол-во уравнений, имеющих 1 корень | Кол-во уравнений, не имеющих корней |
б) Каков объём проведённого измерения?
в) Какова процентная частота уравнений, не имеющих корней?
Задание № 34.5. Уравнение относительно переменной х имеет вид ах + b/x + с = 0, где коэффициенты а, b – натуральные числа от 1 до 5 (совпадения допустимы), а коэффициент с равен 6 или 7.
а) Изобразите схематично дерево вариантов составления уравнений такого вида.
б) Сколько различных уравнений такого вида можно составить?
в) Сколько среди них уравнений, у которых а = b?
г) Сколько среди них уравнений, у которых с = 2а?
Задание № 34.6. Вот что прочёл богатырь на камне у распутья: «Налево, прямо или направо пойдёшь – к таким же распутьям придёшь, а от каждого из них опять к таким же распутьям придёшь, но потом всё равно в тридевятое царство попадёшь».
а) По скольким путям богатырь может доехать до тридевятого царства?
б) Сколько имеется путей, по которым придётся один раз поворачивать влево и два раза – вправо?
в) Сколько имеется путей, по которым придётся один раз поворачивать вправо и два раза – влево?
г) Сколько имеется путей, по которым придётся поворачивать ровно два раза?
Задание № 34.7. Х–файл расположен в директории «Мои документы», где–то в папках А, В, С или D первого уровня. Папка А содержит «подпапки» АА, АВ, АС второго уровня. Папки В и D также содержат по три «подпапки»: BA, ВВ, ВС и DA, DB, DC соответственно, а в папке С содержатся «подпапки» СА, СВ, СС, CD, СЕ второго уровня. Каждая из папок второго уровня содержит по 7 папок третьего уровня, кроме папки ВС, в которой 8 папок третьего уровня. Все папки третьего уровня содержат только файлы. Пользователь решил найти Х–файл прямым перебором всех файлов во всех папках.
а) Изобразите схематично соответствующее дерево вариантов прохождения путей до файла,
б) Сколькими путями можно из папки А дойти до файла?
в) Сколькими путями можно из папки «Мои документы» дойти до файла?
г) Какова вероятность того., что нужный файл окажется в папке С?
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. § 34. Комбинаторные и вероятностные задачи к главе 4. ОТВЕТЫ на упражнения 34.1 — 34.7. Вернуться в ОГЛАВЛЕНИЕ.