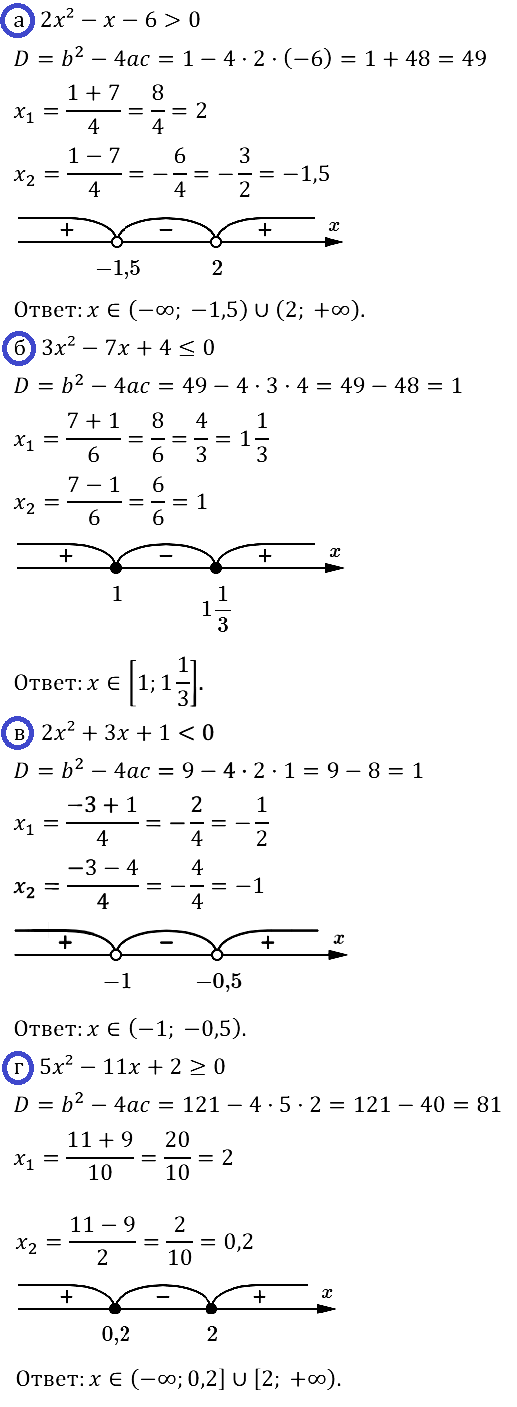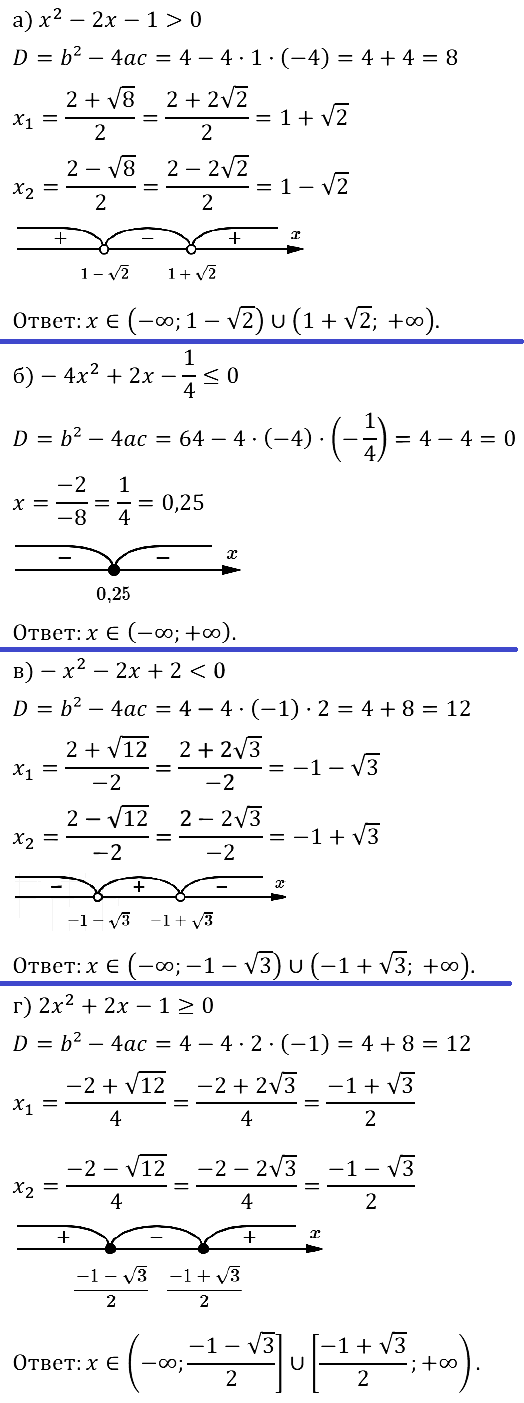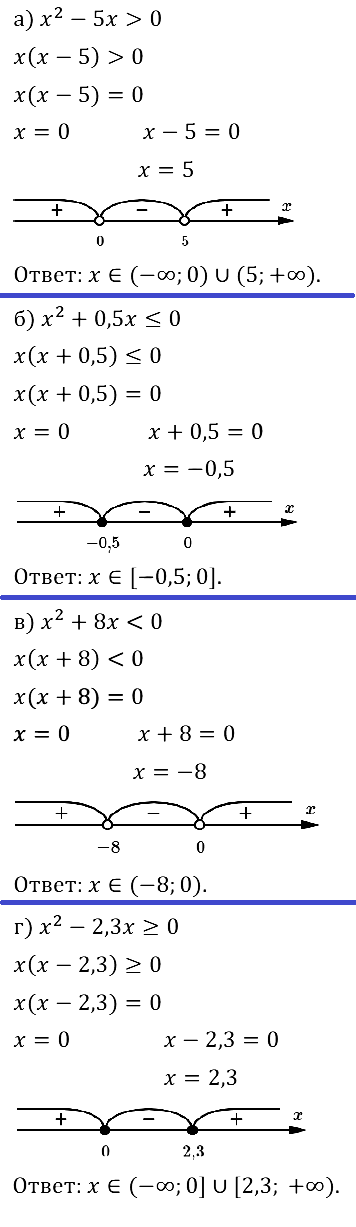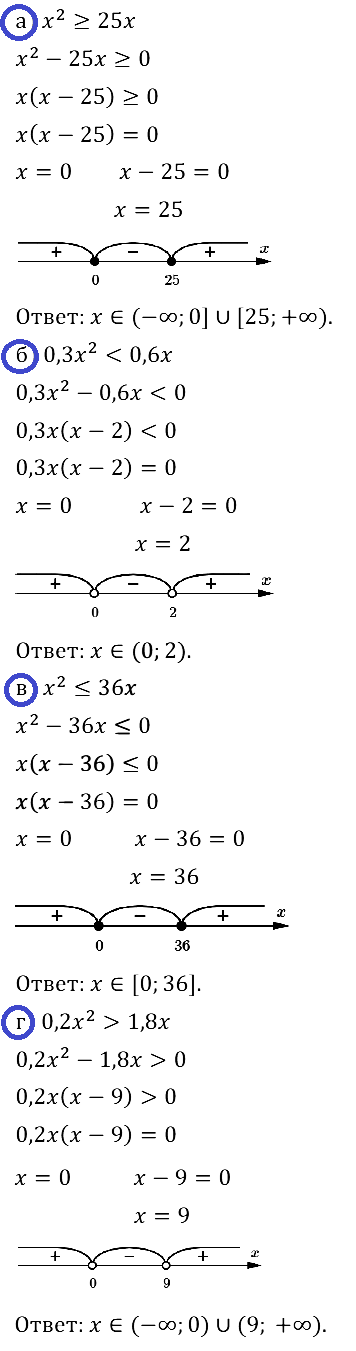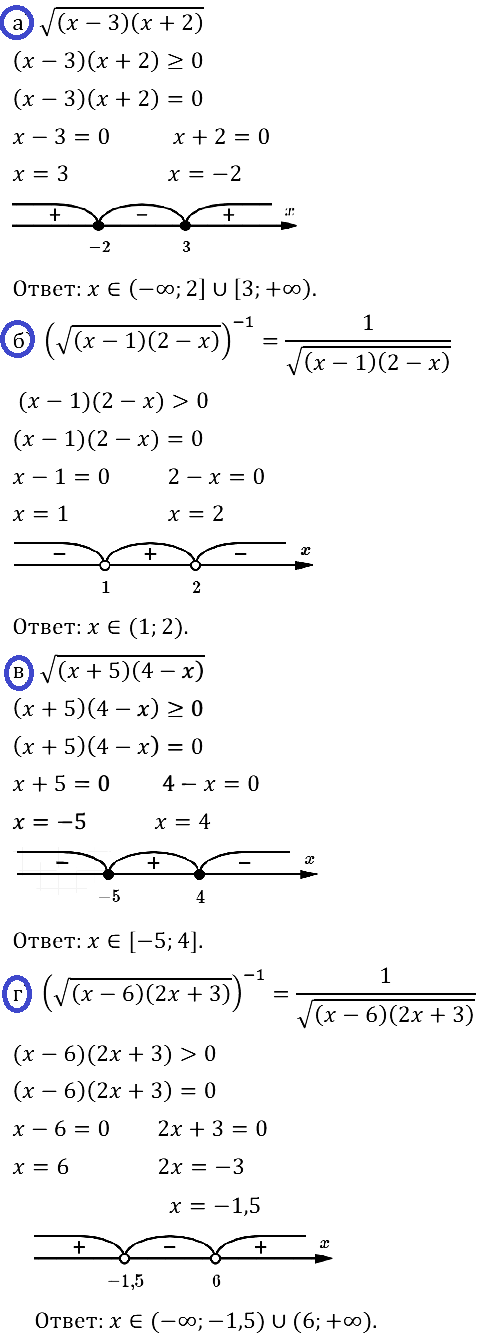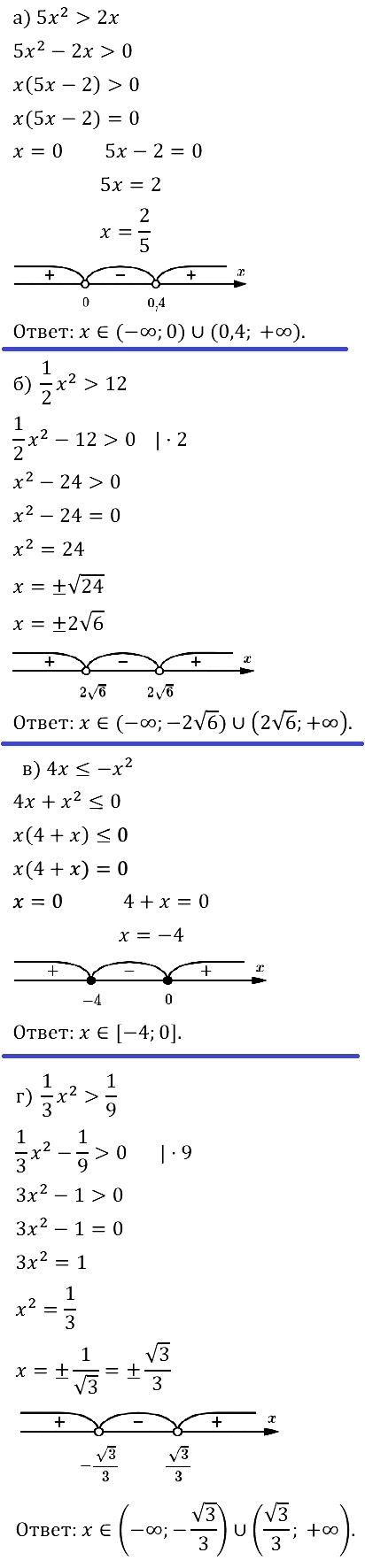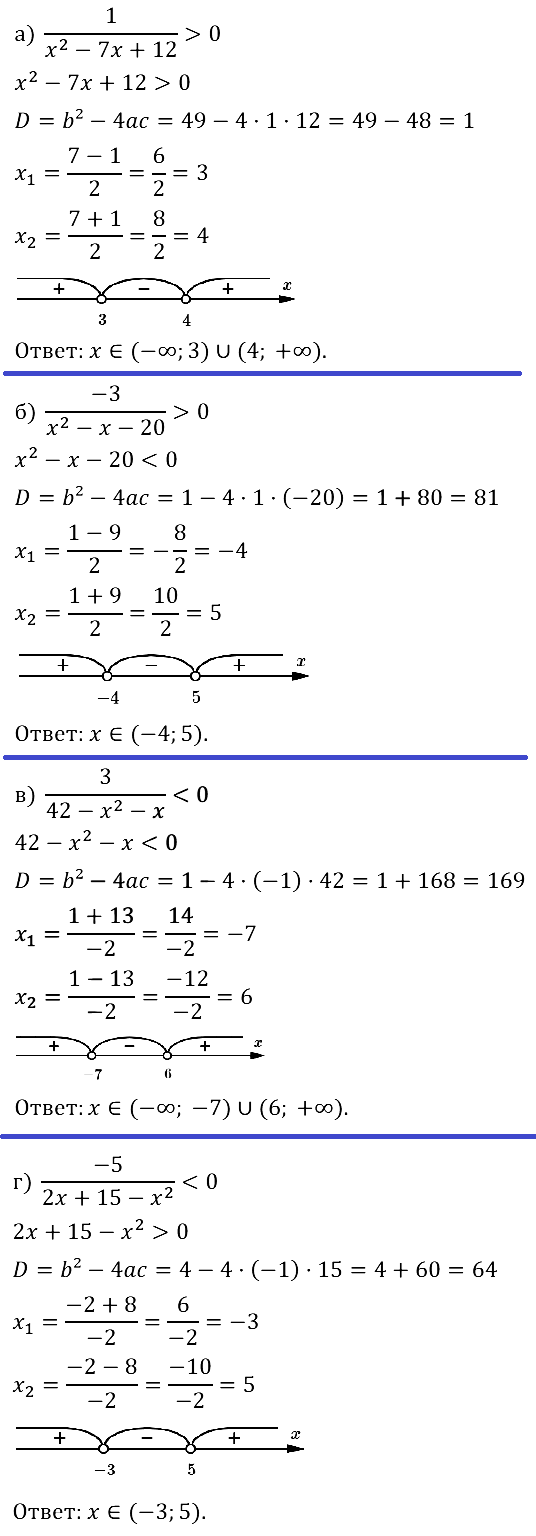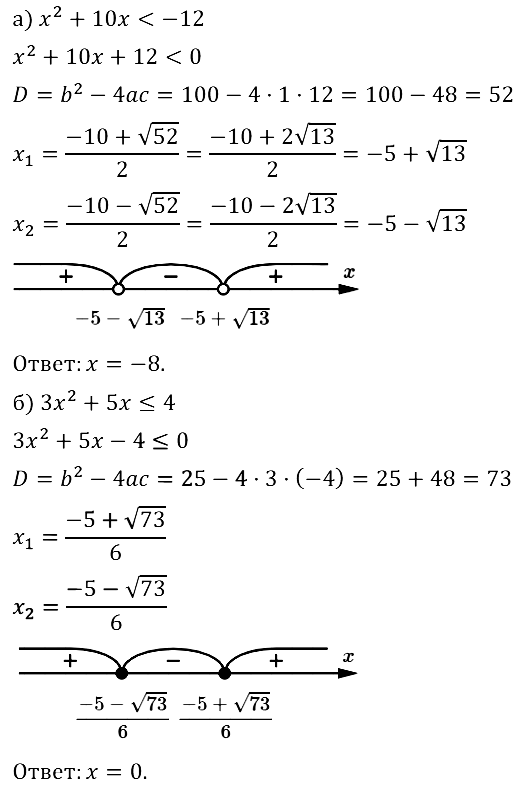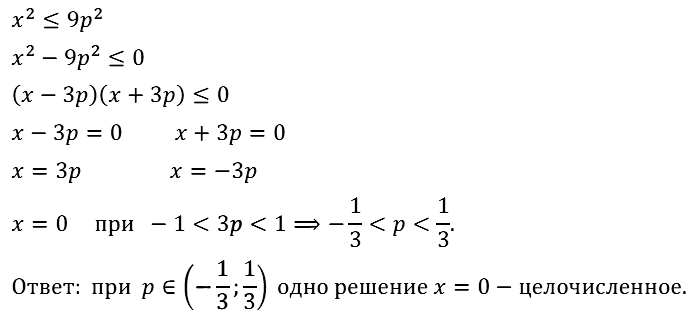Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). § 37. Решение квадратных неравенств. ОТВЕТЫ на упражнения 37.1 — 37.46. ГЛАВА 5. НЕРАВЕНСТВА. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 37.1 — 37.46)
§ 37. Решение квадратных неравенств.
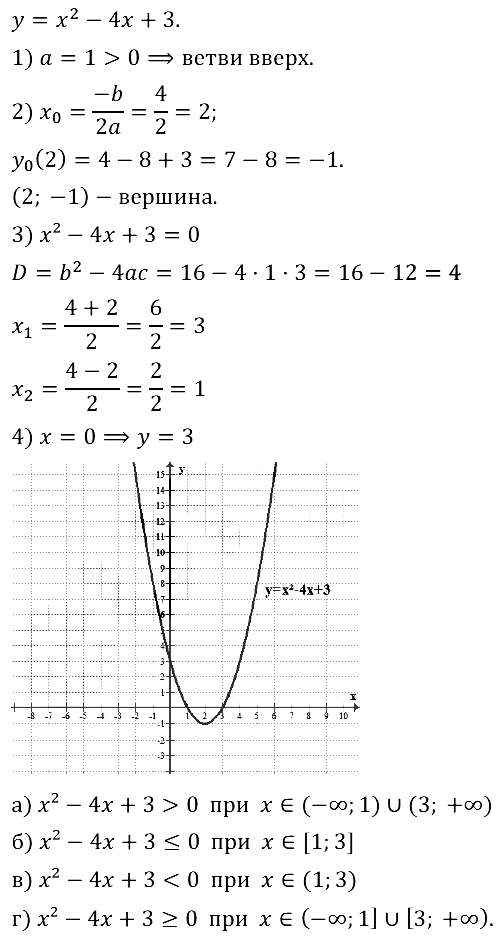
Задание № 37.1. Постройте график функции у = x2 – 4х + 3. С помощью графика решите неравенство:
а) x2 – 4х + 3 > 0; б) x2 – 4х + 3 ≤ 0; в) x2 – 4х + 3 < 0; г) х2 – 4х + 3 ≥ 0.
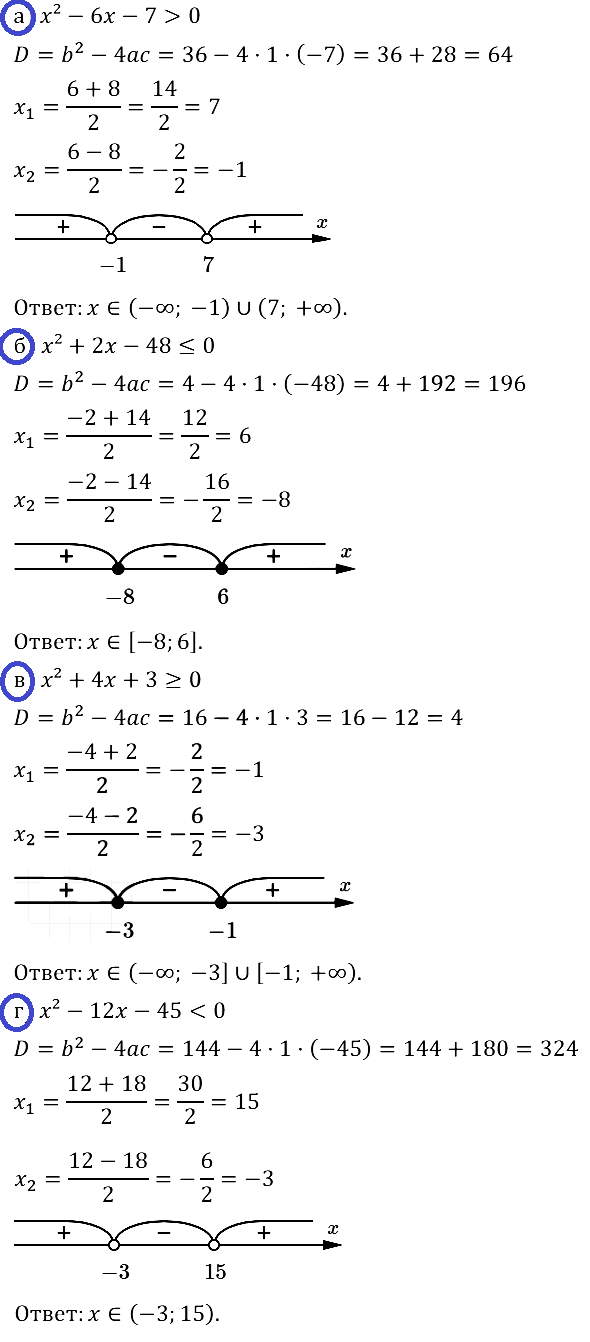
Задание № 37.2. Решите неравенство:
а) x2 – 6х – 7 > 0; б) x2 + 2х – 48 ≤ 0; в) x2 + 4х + 3 ≥ 0; г) x2 – 12x – 45 < 0.
Решите неравенство:
Задание № 37.3. а) –x2 + 6x – 5 < 0; б) –x2 – 2х + 8 ≥ 0; в) –x2 + 16x – 28 > 0; г) –x2 + 4x – 3 < 0.
Задание № 37.4. а) 2x2 – х – 6 > 0; б) 3x2 – 7x + 4 ≤ 0; в) 2x2 + 3x + 1 < 0; г) 5x2 – 11x + 2 ≥ 0.
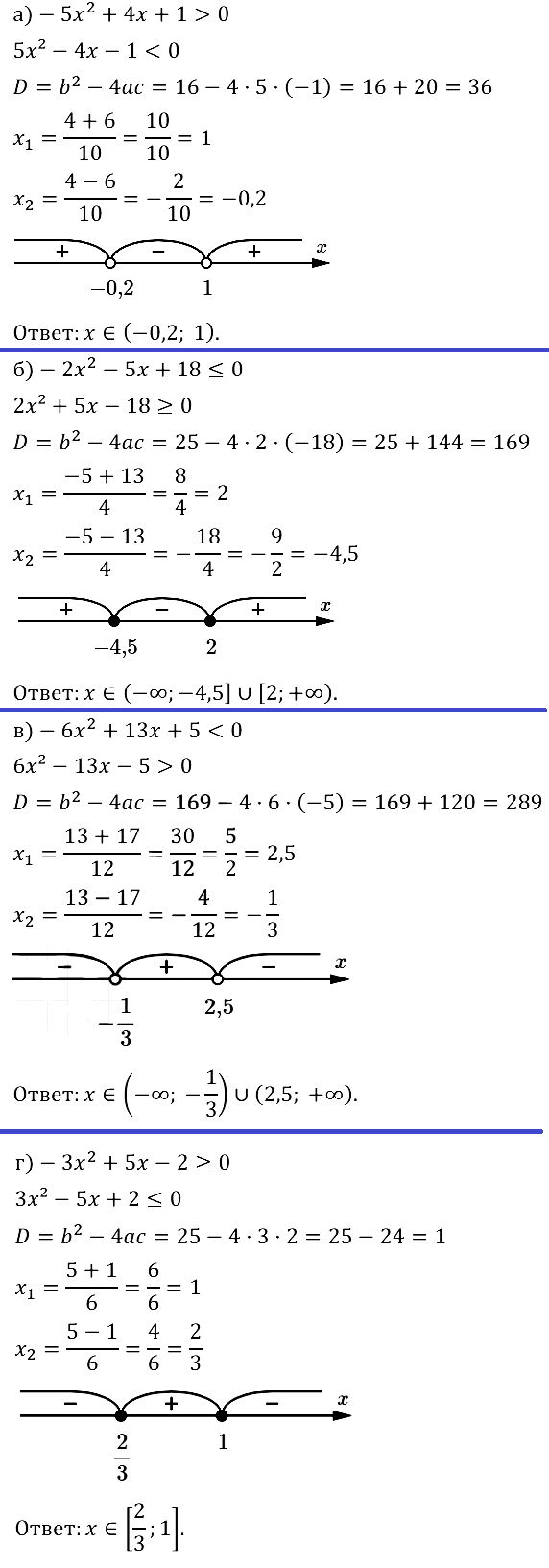
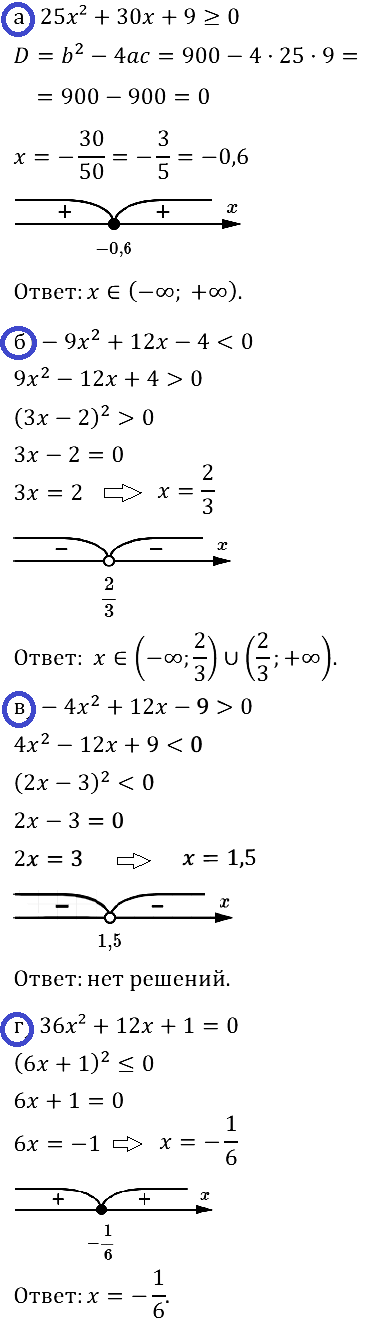
Задание № 37.5. а) –5x2 + 4x + 1 > 0; б) –2x2 – 5x + 18 ≤ 0; в) –6x2 + 13x + 5 < 0; г) –3x2 + 5x – 2 ≥ 0.
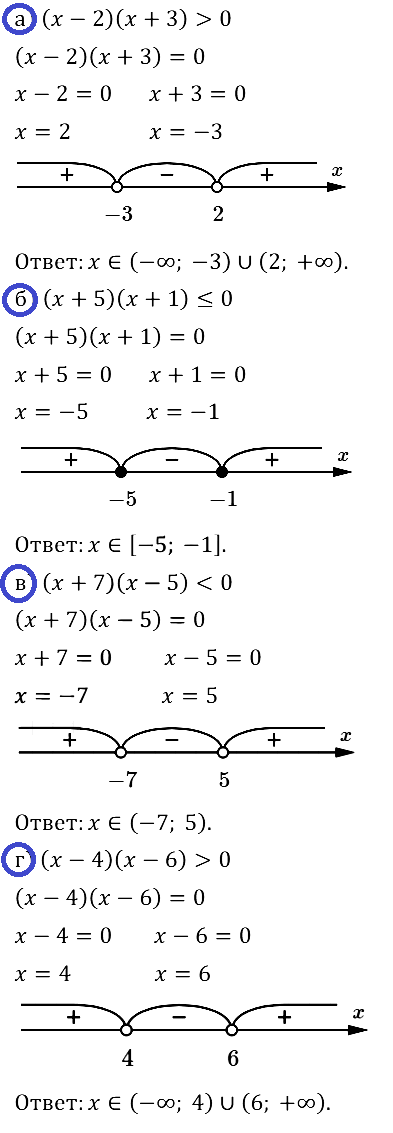
Задание № 37.6. а) (x – 2)(x + 3) > 0; б) (x + 5)(x + 1) ≤ 0; в) (x + 7)(x – 5) < 0; г) (x – 4)(x – 6) > 0.
Задание № 37.7.
Задание № 37.8.
Задание № 37.9.
Задание № 37.10.
Задание № 37.11.
Задание № 37.12.
Задание № 37.13.
Задание № 37.14.
Задание № 37.15.
Задание № 37.16.
Задание № 37.17.
Задание № 37.18.
Задание № 37.19. Решите неравенство: а) x2 ≥ 25x; б) 0,3x2 < 0,6x; в) x2 ≤ 36x; г) 0,2x2 > 1,8x.
Задание № 37.20. При каких значениях x:
а) трехчлен 2x2 + 5x + 3 принимает положительные значения;
б) трехчлен –x2 – x/3 – 1/36 принимает неотрицательные значения?
Задание № 37.21. а) Сколько целочисленных решений имеет неравенство x2 – 5x – 6 < 0?
б) Сколько целочисленных решений имеет неравенство x2 – 6x ≤ 7?
Задание № 37.22. а) Найдите наименьшее целочисленное решение неравенства x2 + 7x ≤ 30.
б) Найдите наибольшее целочисленное решение неравенства 3x – x2 > –40.
Задание № 37.23.
Задание № 37.24.
Задание № 37.25.
Задание № 37.26.
Задание № 37.27.
Задание № 37.28.
Задание № 37.29.
Задание № 37.30.
Задание № 37.31.
Задание № 37.32.
Задание № 37.33.
Задание № 37.34. а) Сколько целочисленных решений имеет неравенство x2 + 5х – 8 < 0?
б) Сколько целочисленных решений имеет неравенство 15 – x2 + 10х > 0?
Задание № 37.35. а) Найдите наименьшее целочисленное решение неравенства x2 + 10х < –12.
б) Найдите наибольшее целочисленное решение неравенства 3x2 + 5х ≤ 4.
Задание № 37.36. При каких значениях параметра р квадратное уравнение 3x2 – 2рх – р + 6 = 0:
а) имеет два различных корня; б) имеет один корень; в) не имеет корней?
Задание № 37.37. При каких значениях параметра р квадратное уравнение 2x2 – 2рх + р + 12 = 0:
а) имеет два различных корня; б) имеет один корень; в) не имеет корней?
Задание № 37.38. При каких значениях параметра р квадратное уравнение x2 + 6рх + 9 = 0:
а) имеет два различных корня; б) имеет один корень; в) не имеет корней?
Задание № 37.39. Найдите все значения параметра р, при которых не имеет действительных корней уравнение:
а) (р – 1)x2 – 4х + 5 = 0;
б) (р – 15)x2 + 4px – 3 = 0;
в) (2p + 3)x2 – 6х + 8 = 0;
г) (3p – 5)x2 – (6p – 2)х + 3p – 2 = 0.
Задание № 37.40. Найдите все значения параметра р, при которых имеет действительные корни уравнение:
а) x2 – 6х + p2 = 0; б) x2 – 12px – 3p = 0; в) x2 – 4х – 2p = 0; г) x2 + 2px + р + 2 = 0.
Задание № 37.41. Найдите все значения параметра р, при которых имеет действительные корни уравнение:
а) 3px2 – 6px + 13 = 0;
б) (1 – 3p)x2 – 4х – 3 = 0;
в) px2 – 3рх – 2 = 0;
г) (р – 1)x2 – (2p – 3)х + р + 5 = 0.
Задание № 37.42. При каких целочисленных значениях параметра р неравенство (х – 2)(х – р) < 0 имеет три целочисленных решения?
Задание № 37.43. При каких значениях параметра р неравенство x2 ≤ 9р2 имеет одно целочисленное решение?
Задание № 37.44. Длина прямоугольника на 2 см больше его ширины. Чему равна длина прямоугольника, если известно, что его площадь не превосходит 224 см2?
Задание № 37.45. Непараллельные стороны квадрата увеличили на 6 см и 4 см. Чему равна сторона квадрата, если известно, что площадь полученного прямоугольника меньше удвоенной площади квадрата?
Задание № 37.46. Две группы туристов вышли с турбазы по направлениям, которые образуют прямой угол. Первая группа шла со скоростью 4 км/ч, а вторая со скоростью 5 км/ч. Группы поддерживали связь по радио, причем переговариваться можно было на расстоянии не более чем 13 км. Какое время после выхода второй группы могли поддерживать между собой связь туристы, если известно, что вторая группа вышла на маршрут через 2 ч после первой?
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). ГЛАВА 5. НЕРАВЕНСТВА. § 37. Решение квадратных неравенств. ОТВЕТЫ на задачи 37.1 — 37.46. Вернуться в ОГЛАВЛЕНИЕ.