Упражнения 371 — 398 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 2. Параллелограмм и трапеция (43. Параллелограмм. 44. Признаки параллелограмма. 45. Трапеция). Геометрия 8 класс Атанасян Задачи 371-398 + ОТВЕТЫ.
Вернуться в ОГЛАВЛЕНИЕ учебника
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. § 2. Параллелограмм и трапеция
Задачи №№ 371 — 398:
Задача № 371. □ Докажите, что выпуклый четырёхугольник ABCD является параллелограммом, если: a) ∠BAC = ∠ACD и ∠BCA = ∠DАС; б) АВ||CD, ∠A = ∠C. .
Задача № 372. Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если: а) одна сторона на 3 см больше другой; б) разность двух сторон равна 7 см; в) одна из сторон в два раза больше другой. .
Задача № 373. Периметр параллелограмма ABCD равен 50 см, ∠C = 30°, а перпендикуляр ВН к прямой CD равен 6,5 см. Найдите стороны параллелограмма. .
Задача № 374. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр этого параллелограмма, если ВК = 15 см, КС = 9 см.
Задача № 375. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. .
Задача № 376. Найдите углы параллелограмм: ABCD, если: a) ∠A = 84°; б) ∠A – ∠B = 55°; в) ∠A + ∠C = 142°; г) ∠А = 2∠В; д) ∠CAD = 16°, ∠ACD = 37°. .
Задача № 377. В параллелограмме MNPQ проведён перпендикуляр NH к прямой MQ, причём точка Н лежит на стороне MQ. Найдите стороны и углы параллелограмма, если известно, что МН = 3 см, HQ = 5 см, ∠MNH = 30°. .
Задача № 378. Докажите, что параллелограмм является выпуклым четырёхугольником .
Задача № 379. □ Из вершин В и D параллелограмма ABCD, у которого АВ ≠ ВС и угол А острый, проведены перпендикуляры ВК и DM к прямой АС. Докажите, что четырёхугольник BMDK — параллелограмм. .
Задача № 380. На сторонах АВ, ВС, CD и DA четырёхугольника ABCD отмечены соответственно точки М, N, Р и Q так, что АМ = СР, BN = DQ, BM = DP, NC = QA. Докажите, что ABCD и MNPQ — параллелограммы. .
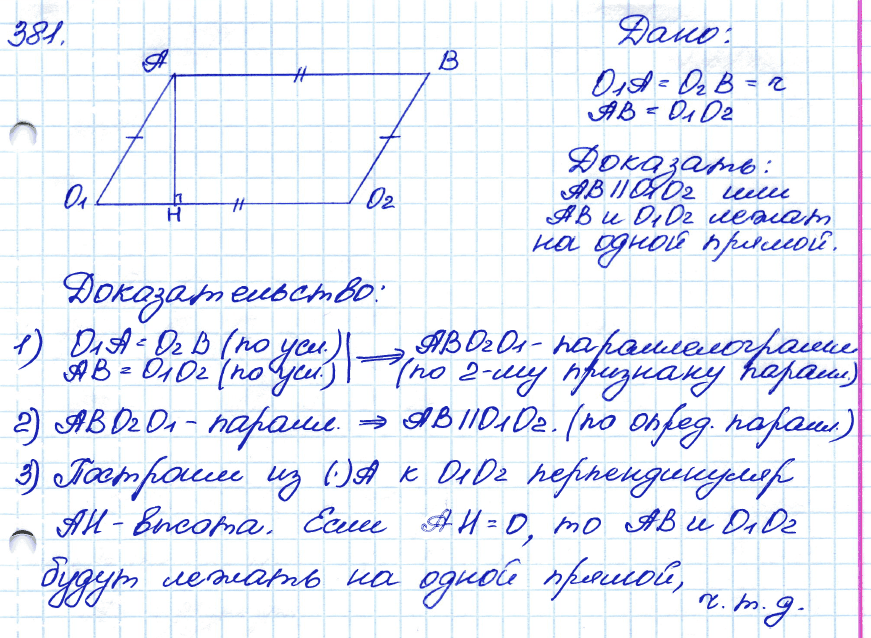
Задача № 381. На рисунке 163 изображены два одинаковых колеса тепловоза. Радиусы О1А и О2В равны. Стержень АВ, длина которого равна расстоянию О1О2 между центрами колёс, передаёт движение от одного колеса к другому. Докажите, что отрезки АВ и О1О2 либо параллельны, либо лежат на одной прямой. .
Задача № 382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырёхугольник A1B1C1D1, вершинами которого являются середины отрезков ОА, ОВ, ОС и OD, — параллелограмм. .
Задача № 383. На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что РВ = QD. Докажите, что четырёхугольник APCQ — параллелограмм. .
Задача № 384. Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.
Задача № 385. Докажите теорему Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Задача № 386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции. .
Задача № 387. Найдите углы В и D трапеции ABCD с основаниями AD и ВС, если ∠A = 36°, ∠C =117°. .
Задача № 388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны; б) диагонали равны. .
Задача № 389. Докажите, что трапеция равнобедренная, если: а) углы при основании равны; б) диагонали трапеции равны. .
Задача № 390. Один из углов равнобедренной трапеции равен 68°. Найдите остальные углы трапеции. .
Задача № 391. Докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости. .
Задача № 392. □ Основания прямоугольной трапеции равны а и b, один из углов равен α. Найдите: а) большую боковую сторону трапеции, если а = 4см, b = 7см, α = 60°; б) меньшую боковую сторону трапеции, если а = 10 см, b = 15 см, α = 45°. .
Задача № 393. □ Постройте параллелограмм: а) по двум смежным сторонам и углу между ними; б) по двум диагоналям и углу между ними; в) по двум смежным сторонам и соединяющей их концы диагонали.
Задача № 394. Даны три точки А, B и С, не лежащие на одной прямой. Постройте параллелограмм так, чтобы три его вершины совпадали с данными точками. Сколько таких параллелограммов можно построить? .
Задача № 395. Даны острый угол hk и два отрезка P1Q1 и P2Q2. Постройте параллелограмм ABCD так, чтобы расстояние между параллельными прямыми АВ и DC равнялось P1Q1, AB = P2Q2 и ∠A = ∠hk.
Задача № 396. Разделите данный отрезок АВ на п равных частей
Задача № 397. □ Постройте равнобедренную трапецию ABCD: а) по основанию AD, углу А и боковой стороне АВ; б) по основанию ВС, боковой стороне АВ и диагонали BD.
Задача № 398. □ Постройте прямоугольную трапецию ABCD по основаниям и боковой стороне AD, перпендикулярной к основаниям.
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 2. Параллелограмм и трапеция. Геометрия 8 класс Атанасян Задачи 371-398 + ОТВЕТЫ.