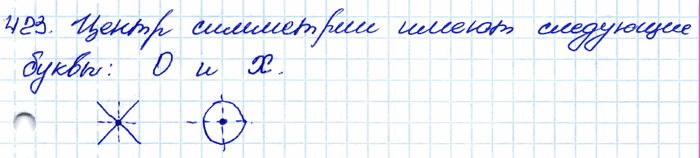Упражнения 399 — 423 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии). Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Вернуться в ОГЛАВЛЕНИЕ учебника
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. § 3. Прямоугольник, ромб, квадрат
Задачи №№ 399 — 423:
Задача № 399. □ Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.
Задача № 400. □ Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.
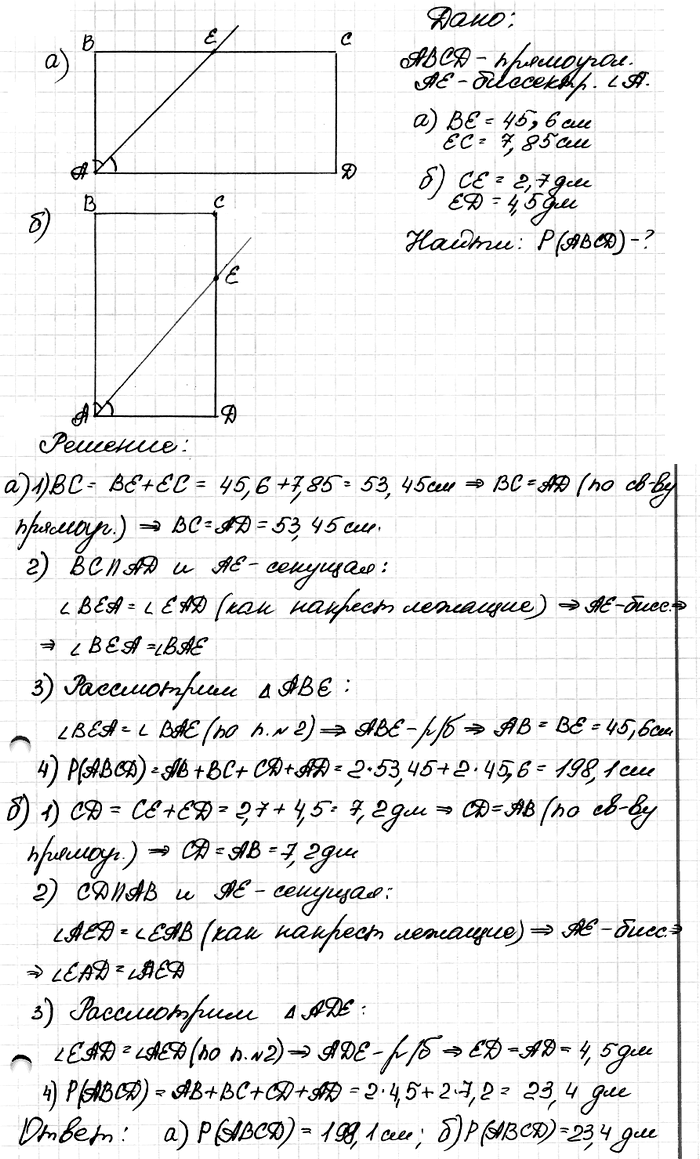
Задача № 401. Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см; б) DC на отрезки 2,7 дм и 4,5 дм.
Задача № 402. □ Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники AOD и АОВ равнобедренные.
Задача № 403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если ∠CAD = 30°, АС = 12 см.
Задача № 404. □ Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
Задача № 405. □ В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.
Задача № 406. Найдите периметр ромба ABCD, в котором ∠B = 60°, АС= 10,5 см.
Задача № 407. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.
Задача № 408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.
Задача № 409. □ Докажите, что ромб, у которого один угол прямой, является квадратом.
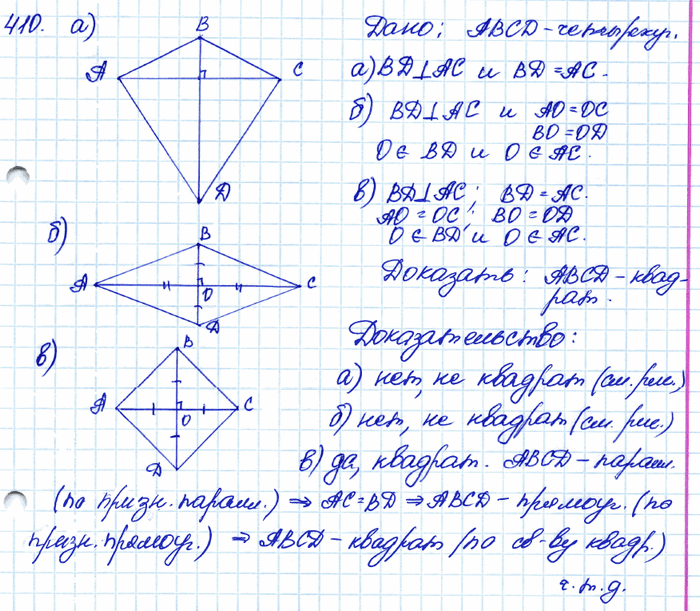
Задача № 410. □ Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?
Задача № 411. □ В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник — квадрат.
Задача № 412. Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС = 12см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите периметр квадрата.
Задача № 413. □ Постройте прямоугольник: а) по двум смежным сторонам; б) по стороне и диагонали; в) по диагонали и углу между диагоналями.
Задача № 414. □ Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
Задача № 415. □ Постройте квадрат: а) по стороне; б) по диагонали.
Задача № 416. □ Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
Задача № 417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
Задача № 418. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F ?
Задача № 419. □ Докажите, что прямая, проходящая через середины противоположных сторон прямоугольника, является его осью симметрии.
Задача № 420. □ Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.
Задача № 421. □ Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.
Задача № 422. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
Задача № 423. Какие из следующих букв имеют центр симметрии: А, О, М, X, К?
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат. Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.