Упражнения 424 — 444 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. Дополнительные задачи к главе V. Геометрия 8 класс Атанасян Задачи 424-444 + ОТВЕТЫ.
Вернуться в ОГЛАВЛЕНИЕ учебника
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. Дополнительные задачи к главе.
Задачи №№ 424-444:
Задача № 424. Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.
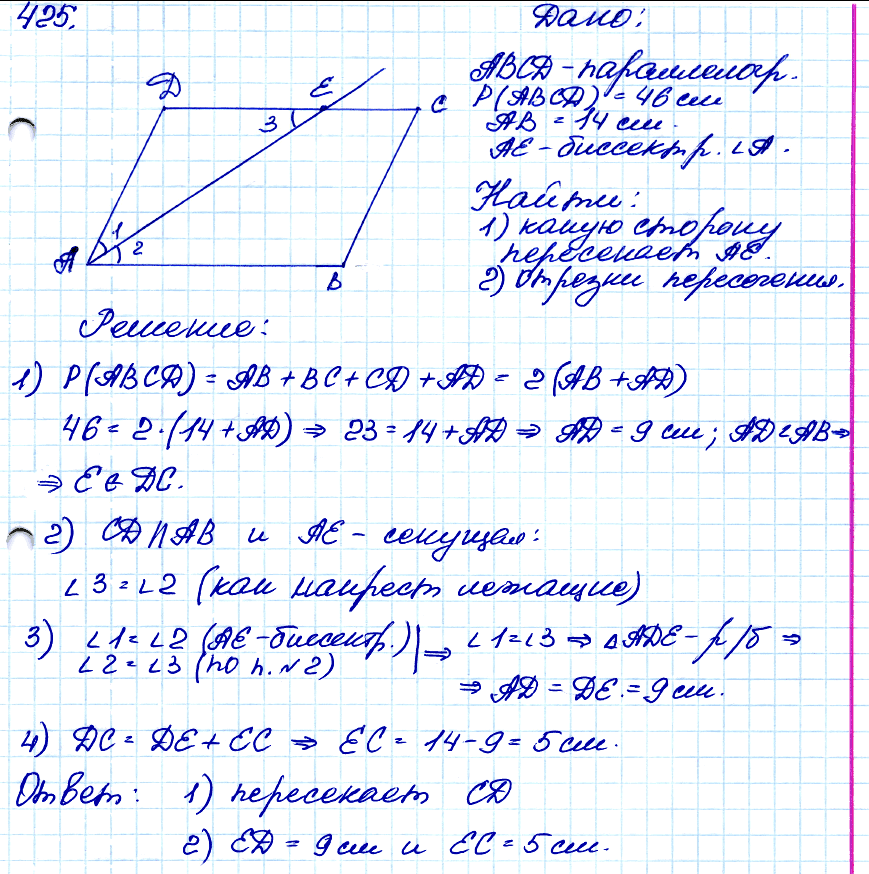
Задача № 425. Периметр параллелограмма ABCD равен 46 см, АВ = 14 см. Какую сторону параллелограмма пересекает биссектриса угла А? Найдите отрезки, которые образуются при этом пересечении.
Задача № 426. Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.
Задача № 427. Через произвольную точку основания равнобедренного треугольника проведены прямые, параллельные боковым сторонам треугольника. Докажите, что периметр получившегося четырёхугольника равен сумме боковых сторон данного треугольника.
Задача № 428. В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.
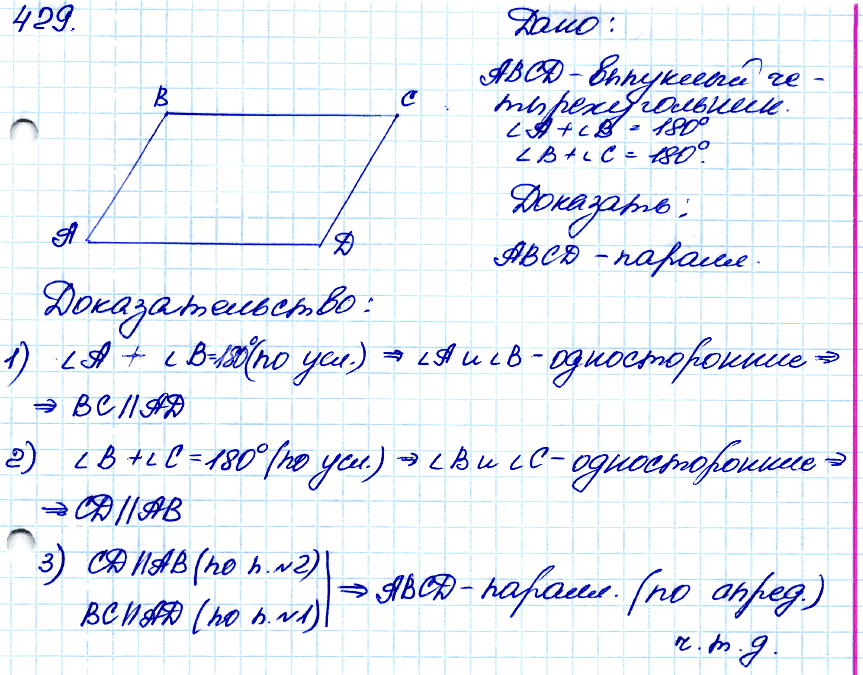
Задача № 429. Докажите, что выпуклый четырёхугольник является параллелограммом, если сумма углов, прилежащих к каждой из двух смежных сторон, равна 180°.
Задача № 430. Докажите, что выпуклый четырёхугольник является параллелограммом, если его противоположные углы попарно равны.
Задача № 431. Точка К — середина медианы AM треугольника АВС. Прямая ВК пересекает сторону АС в точке D. Докажите, что AD = 1/3 • АС.
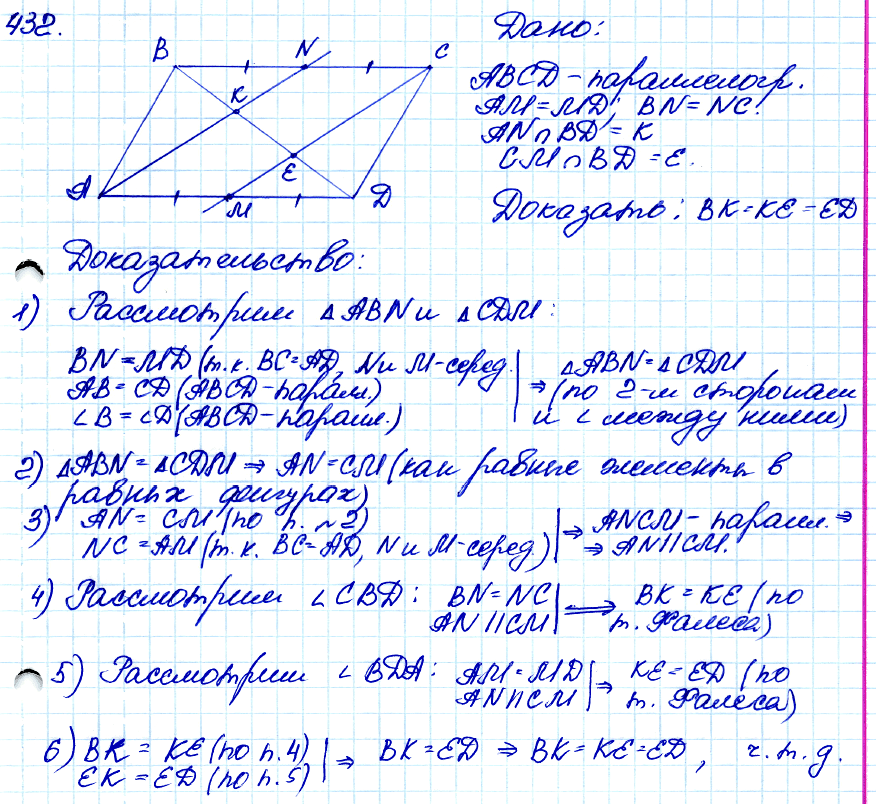
Задача № 432. Точки М и N — середины сторон AD и ВС параллелограмма ABCD. Докажите, что прямые AN и МС делят диагональ BD на три равные части.
Задача № 433. Из вершины В ромба ABCD проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что луч BD является биссектрисой угла КВМ.
Задача № 434. Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон.
Задача № 435. Докажите, что середина отрезка, соединяющего вершину треугольника с любой точкой противоположной стороны, лежит на отрезке с концами в серединах двух других сторон.
Задача № 436. Диагональ АС квадрата ABCD равна 18,4 см. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и CD соответственно в точках М и N. Найдите MN.
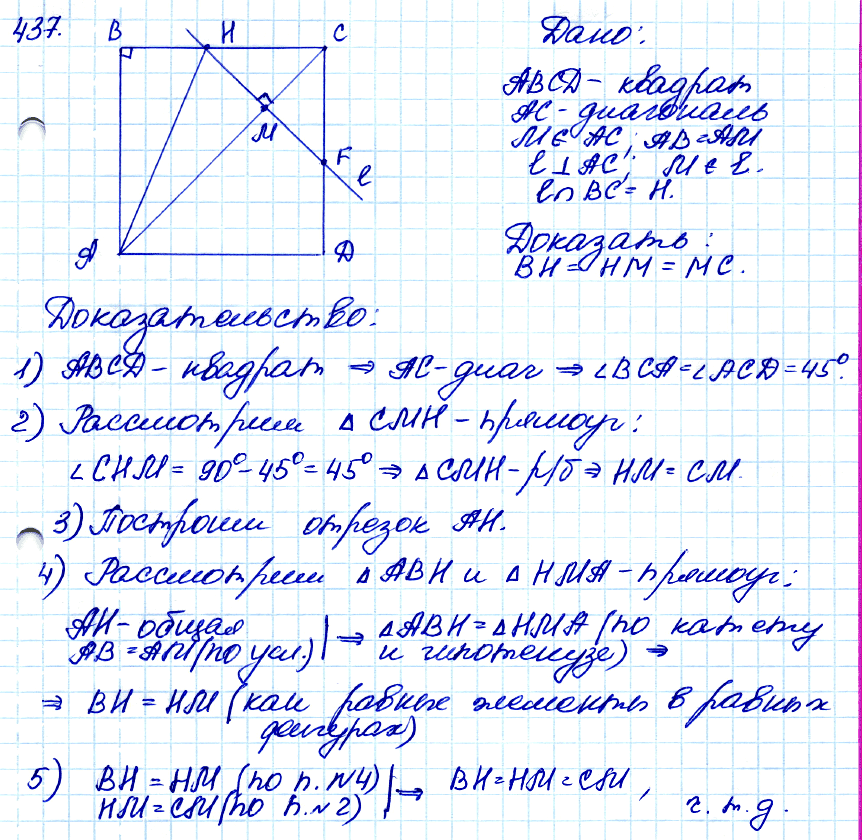
Задача № 437. На диагонали АС квадрата ABCD взята точка М так, что АМ = АВ. Через точку М проведена прямая, перпендикулярная к прямой АС и пересекающая ВС в точке Н. Докажите, что ВН = НМ = МС.
Задача № 438. В трапеции ABCD с большим основанием AD диагональ АС перпендикулярна к боковой стороне CD, ∠B АС = ∠CAD. Найдите AD, если периметр трапеции равен 20 см, a ∠D = 60°.
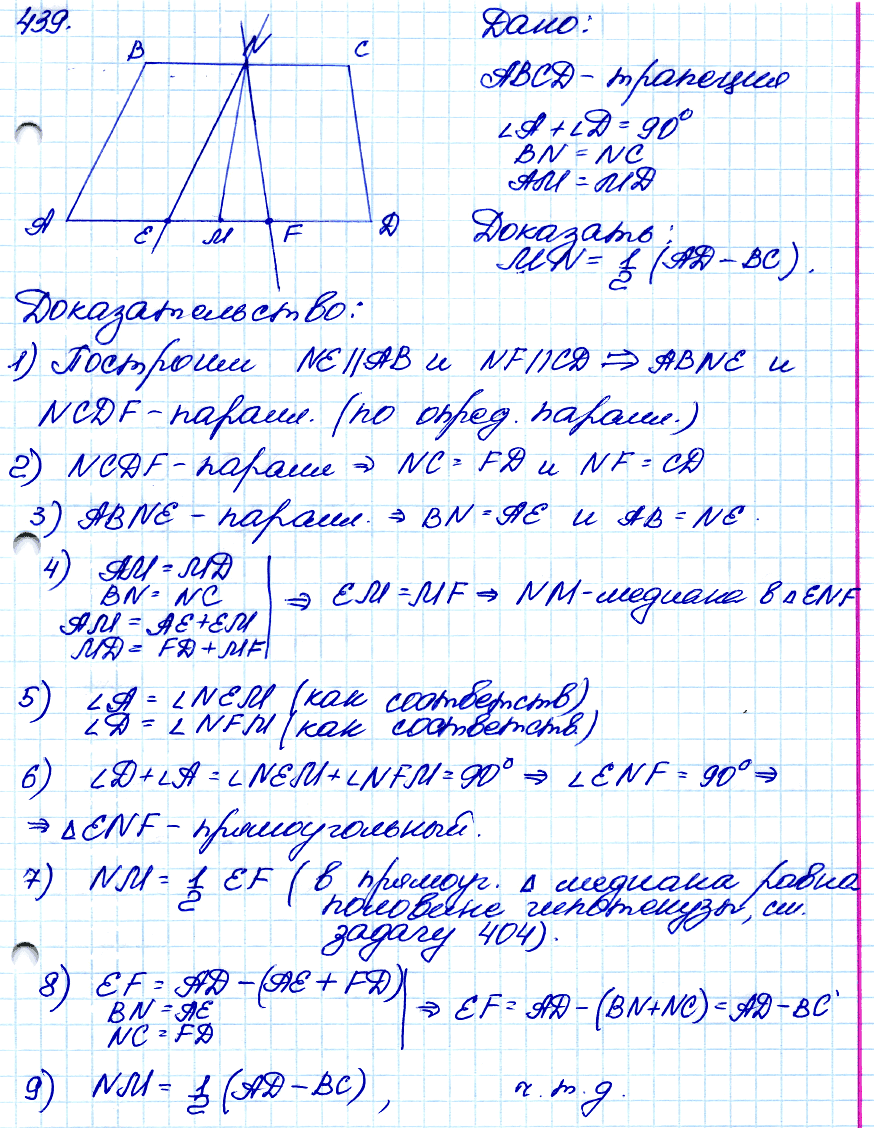
Задача № 439. * □ Сумма углов при одном из оснований трапеции равна 90°. Докажите, что отрезок, соединяющий середины оснований трапеции, равен их полуразности.
Задача № 440. * □ На двух сторонах треугольника вне его построены квадраты. Докажите, что отрезок, соединяющий концы сторон квадратов, выходящих из одной вершины треугольника, в два раза больше медианы треугольника, выходящей из той же вершины.
Задача № 441. Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.
Задача № 442. Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.
Задача № 443. Сколько центров симметрии имеет пара параллельных прямых?
Задача № 444. * □ Докажите, что если фигура имеет две взаимно перпендикулярные оси симметрии, то точка их пересечения является центром симметрии фигуры.
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. Дополнительные задачи к главе V. Геометрия 8 класс Атанасян Задачи 424-444 + ОТВЕТЫ.