Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Первый признак подобия треугольников». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Первый признак подобия треугольников
Вариант 1
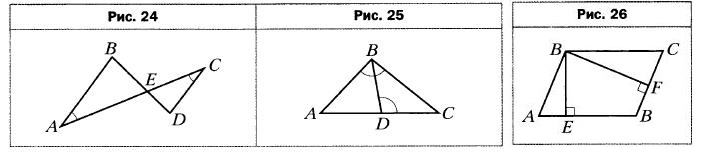
- На рисунке 24 ∠BAC = ∠ACD. Подобны ли треугольники АВЕ и CDE? В случае положительного ответа укажите пары соответственных сторон.
- На рисунке 25 ∠ABC = ∠BDC. Найдите подобные треугольники на рисунке и докажите их подобие.
- В параллелограмме ABCD проведены высоты BE и BF (рис. 26). Докажите подобие треугольников АВЕ и CBF.
- Стороны параллелограмма равны 15 см и 30 см, а расстояние между меньшими сторонами — 20 см. Найдите расстояние между большими сторонами параллелограмма.
- Периметр параллелограмма равен 70 см, а его высоты — 3 см и 4 см. Найдите стороны параллелограмма.
- Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Найдите отрезки, на которые точка пересечения диагоналей делит данную диагональ.
- В трапеции ABCD (ВС II AD) О — точка пересечения диагоналей, АО : ОС = 5 : 2. Найдите большее основание трапеции, если её средняя линия равна 7 см.
- На стороне А В треугольника АВС отметили точку М так, что ∠ACM = ∠ABC, AM = 9 см, ВМ = 7 см. Найдите сторону АС.
- Хорды МК и PF окружности пересекаются в точке Е. Найдите отрезок EF, если ME = 4 см, ЕК = 3 см, РЕ = 2 см.
- Хорды АВ и CD окружности пересекаются в точке М, AM = 2 см, ВМ = 9 см, а отрезок СМ в 2 раза больше отрезка DM. Найдите отрезки СМ и DM.
- Точка К удалена на 3 см от центра окружности радиуса 5 см. Через точку К проведена хорда длиной 8 см. Найдите отрезки, на которые точка К делит эту хорду.
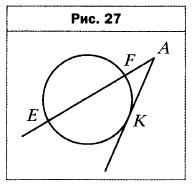
- Через точку А проведены к окружности касательная АК (К — точка касания) и секущая, пересекающая окружность в точках Е и F (рис. 27). Найдите отрезок AF, если АК = 4 см, АЕ = 8 см.
- Через точку К проведены к окружности касательная КА (А — точка касания) и секущая, пересекающая окружность в точках В и С (точка В лежит между точками К и С). Найдите отрезок КВ, если АК = 16 см и КВ : ВС = 1 : 3.
Вариант 2
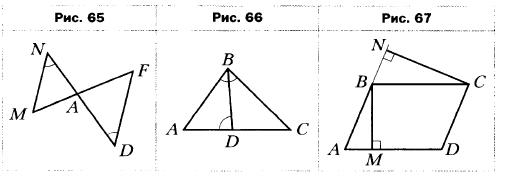
- На рисунке 65 ∠MND = ∠FDN. Подобны ли треугольники MNA и FDA? В случае положительного ответа укажите пары соответственных сторон.
- На рисунке 66 ∠ABC = ∠ADB. Найдите на рисунке подобные треугольники и докажите их подобие.
- В параллелограмме ABCD проведены высоты ВМ и CN (рис. 67). Докажите подобие треугольников АВМ и BCN.
- Расстояния между противолежащими сторонами параллелограмма равны 12 см и 18 см, а его меньшая сторона — 24 см. Найдите большую сторону параллелограмма.
- Периметр параллелограмма равен 64 см, а его высоты — 7 см и 9 см. Найдите стороны параллелограмма.
- Точка пересечения диагоналей трапеции делит одну из диагоналей на отрезки длиной 7 см и 11 см. Найдите основания трапеции, если их разность равна 16 см.
- В трапеции ABCD (ВС II AD) К — точка пересечения диагоналей, АК : КС = 9 : 4, KD – ВК = 10 см. Найдите диагональ BD трапеции.
- На стороне АС треугольника АВС отметили точку D так, что ∠ABD = ∠BCA. Известно, что АВ = 3 см, АС = 6 см. Найдите отрезок AD.
- Хорды АВ и CD окружности пересекаются в точке К. Найдите отрезок АК, если КВ = 8 см, СК = 6 см, KD = 4 см.
- Хорды АВ и CD окружности пересекаются в точке К, СК = 6 см, DK = 8 см, а отрезок АК в 3 раза больше отрезка ВК. Найдите отрезки АК и ВК.
- Точка Е удалена на 6 см от центра окружности радиуса 10 см. Через точку Е проведена хорда длиной 16 см. Найдите отрезки, на которые точка Е делит эту хорду.
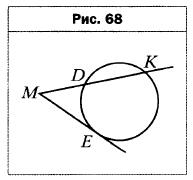
- Через точку М проведены к окружности касательная ME (Е — точка касания) и секущая МК, пересекающая окружность в точках К и D (рис. 68). Найдите отрезок МК, если ME = 6 см, MD = 4 см.
- Через точку М проведены к окружности касательная МА (А — точка касания) и секущая, пересекающая окружность в точках В и С (точка В лежит между точками М и С). Найдите отрезок МВ, если AM = 18 см и МВ : ВС = 4 : 5.
Вариант 3
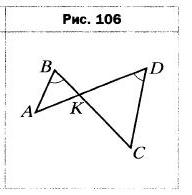
- На рисунке 106 ∠ABC = ∠ADC. Подобны ли треугольники АВК и CDK? В случае положительного ответа укажите пары соответственных сторон.
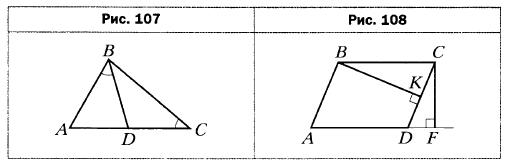
- На рисунке 107 ∠ABD = ∠ACB. Найдите на рисунке подобные треугольники и докажите их подобие.
- В параллелограмме ABCD проведены высоты ВК и CF (рис. 108). Докажите подобие треугольников СВК и DCF.
- Стороны параллелограмма равны 15 см и 20 см, а расстояние между большими сторонами — 12 см. Найдите расстояние между меньшими сторонами параллелограмма.
- Периметр параллелограмма равен 44 см, а его высоты — 5 см и 6 см. Найдите стороны параллелограмма.
- Основания трапеции равны 6 см и 14 см, а одна из диагоналей — 20 см. Найдите отрезки, на которые точка пересечения диагоналей делит данную диагональ.
- В трапеции ABCD (ВС || AD) М — точка пересечения диагоналей, ВМ : MD = 1 : 3. Найдите меньшее основание трапеции, если её средняя линия равна 8 см.
- На стороне ВС треугольника АВС отметили точку К так, что ∠CAK = ∠ABC, СК = 4 см, КВ = 5 см. Найдите сторону АС.
- Хорды PN и SF окружности пересекаются в точке М. Найдите отрезок MN, если РМ = 6 см, SM = 8 см, FM = = 9 см.
- Хорды АВ и CD окружности пересекаются в точке Е, АЕ = 4 см, BE = 9 см, а отрезок СЕ в 4 раза меньше отрезка DE. Найдите отрезки СЕ и DE.
- Точка Р удалена на 12 см от центра окружности радиуса 15 см. Через точку Р проведена хорда длиной 18 см. Найдите отрезки, на которые точка Р делит эту хорду.
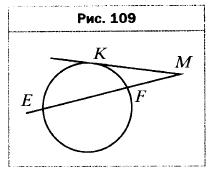
- Через точку М проведены к окружности касательная МК (К — точка касания) и секущая ME, пересекающая окружность в точках Е и F (рис. 109). Найдите отрезок MF, если МК = 10 см, ME = 20 см.
- Через точку F проведены к окружности касательная ЕA (А — точка касания) и секущая, пересекающая окружность в точках В и С (точка В лежит между точками F и С). Найдите отрезок FB, если AF = 24 см и FB : ВС = 9 : 7.
Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Первый признак подобия треугольников». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!