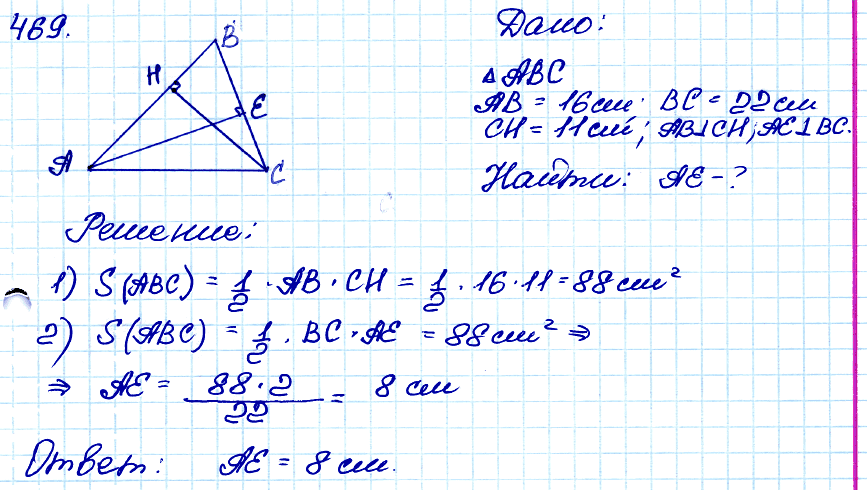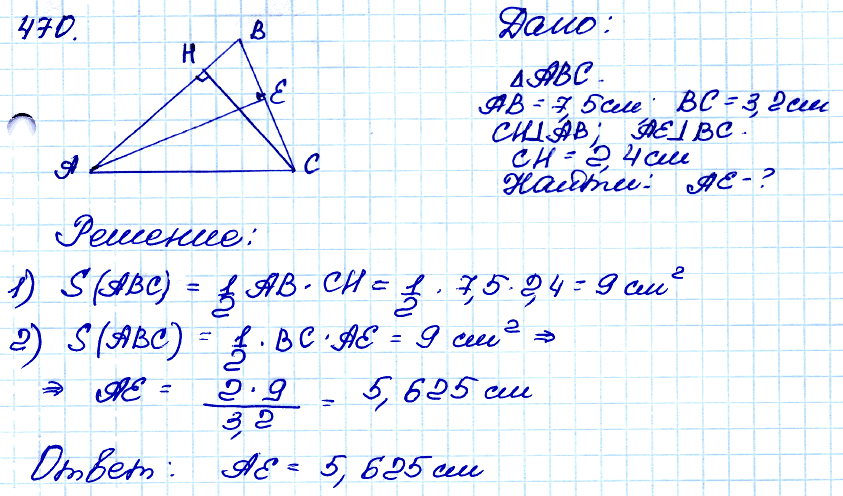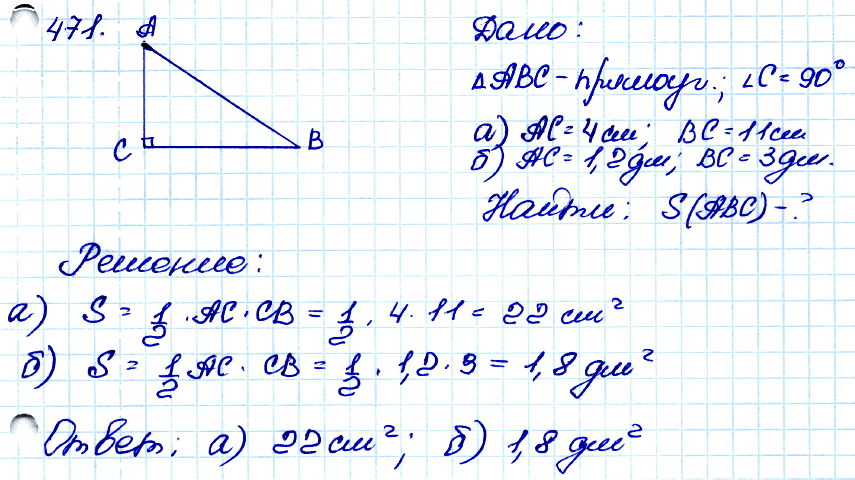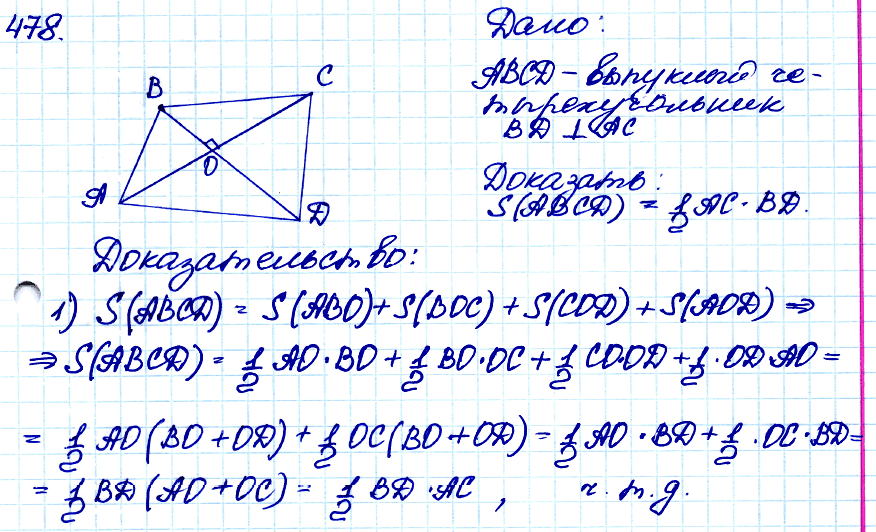Упражнения 459-482 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.
Вернуться в ОГЛАВЛЕНИЕ учебника
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия Атанасян. Глава 6.
§ 2. Площади параллелограмма,
треугольника и трапеции
Задачи №№ 459-482:
Задача № 459. Пусть а — основание, h — высота, a S — площадь параллелограмма. Найдите: a) S, если а = 15 см, h = 12 см; б) а, если S = 34 см2, h = 8,5 см; в) а, если S = 162 см2, h = а/2; г) h, если h = 3а, S = 27.
Задача № 460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
Задача № 461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.
Задача № 462. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.
Задача № 463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма.
Задача № 464. □ Пусть а и b — смежные стороны параллелограмма, S — площадь, a h1 и h2 — его высоты. Найдите: a) h2, если а = 18 см, b = 30 см, h1 = 6 см, h2 > h1; б) h1, если а =10 см, b =15 см, h2 = 6 см, h2 > h1; в) h1 и h2, если S = 54 см2, а = 4,5 см, b = 6 см.
Задача № 465. Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.
Задача № 466. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если большая его сторона равна 15,2 см, а один из его углов 45°.
Задача № 467. Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.
Задача № 468. Пусть а — основание, h — высота, a S — площадь треугольника. Найдите: a) S, если а = 7 см, h = 11 см; б) S, если а = 2√3 см, h = 5 см; в) h, если S = 37,8 см2, а = 14 см; г) а, если S = 12 см2, h = 3√2 см.
Задача № 469. Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведённая к стороне АВ, равна 11 см. Найдите высоту, проведённую к стороне ВС.
Задача № 470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведённая к большей стороне, равна 2,4 см. Найдите высоту, проведённую к меньшей из данных сторон.
Задача № 471. □ Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11 см; б) 1,2 дм и 3 дм.
Задача № 472. Площадь прямоугольного треугольника равна 168 см2. Найдите его катеты, если отношение их длин равно 7/12.
Задача № 473. Через вершину С треугольника АВС проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
Задача № 474. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.
Задача № 475. □ Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.
Задача № 476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм и 14 см; б) 4,6 дм и 2 дм.
Задача № 477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 см2.
Задача № 478. В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.
Задача № 479. Точки D и Е лежат на сторонах АВ и АС треугольника АВС. Найдите: a) SADE, если АВ = 5 см, АС = 6 см, AD = З см, АЕ = 2 см, SABC = 10 см2; б) AD, если АВ = 8 см, АС = З см, АЕ = 2 см, SABC = 10 см2, SADE = 2 см2.
Задача № 480. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 21 см, CD = 17 см, высота ВН равна 7 см;
б) ∠D = 30°, АВ = 2 см, CD = 10 см, DA = 8 см;
в) ВС ⊥ АВ, АВ = 5 см, ВС = 8 см, CD = 13 см.
Задача № 481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.
Задача № 482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведённая из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.